hdu 5120 Intersection 两个圆的面积交

Intersection

Time Limit: 4000/4000 MS (Java/Others)    Memory Limit: 512000/512000 K (Java/Others)

Problem Description

Matt is a big fan of logo design. Recently he falls in love with logo made up by rings. The following figures are some famous examples you may know.

A ring is a 2-D figure bounded by two circles sharing the common center. The radius for these circles are denoted by r and R (r < R). For more details, refer to the gray part in the illustration below.

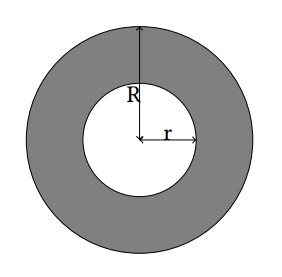
Matt just designed a new logo consisting of two rings with the same size in the 2-D plane. For his interests, Matt would like to know the area of the intersection of these two rings.

 

Input

The first line contains only one integer T (T ≤ 10⁵), which indicates the number of test cases. For each test case, the first line contains two integers r, R (0 ≤ r < R ≤ 10).

Each of the following two lines contains two integers x_i, y_i (0 ≤ x_i, y_i ≤ 20) indicating the coordinates of the center of each ring.

 

Output

For each test case, output a single line “Case #x: y”, where x is the case number (starting from 1) and y is the area of intersection rounded to 6 decimal places.

 

Sample Input

2
2 3
0 0
0 0
2 3
0 0
5 0

 

Sample Output

Case #1: 15.707963
Case #2: 2.250778

 

Source

2014ACM/ICPC亚洲区北京站-重现赛（感谢北师和上交）

题意：求两个圆环的面积交；

思路：圆环的面积交=大圆面积交-2*大小圆面积交+小圆面积交；

#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define fi first
#define se second
#define mkp make_pair
#define eps 1e-8
const double pi=acos(-);
const int N=2e5+,M=1e6+,inf=1e9+;
const LL INF=1e18+,mod=;

int sgn(double x)
{
    if(fabs(x) < eps)return ;
    if(x < )return -;
    else return ;
}
struct Point
{
    double x,y;
    Point() {}
    Point(double _x,double _y)
    {
        x = _x;
        y = _y;
    }
    Point operator -(const Point &b)const
    {
        return Point(x - b.x,y - b.y);
    }
    //叉积
    double operator ^(const Point &b)const
    {
        return x*b.y - y*b.x;
    }
//点积
    double operator *(const Point &b)const
    {
        return x*b.x + y*b.y;
    }
//绕原点旋转角度B（弧度值），后x,y的变化
    void transXY(double B)
    {
        double tx = x,ty = y;
        x= tx*cos(B) - ty*sin(B);
        y= tx*sin(B) + ty*cos(B);
    }
};

double AREA(Point a, double r1, Point b, double r2)
{
    double d = sqrt((a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y));
    if (d >= r1+r2)
        return ;
    if (r1>r2)
    {
        double tmp = r1;
        r1 = r2;
        r2 = tmp;
    }
    if(r2 - r1 >= d)
        return pi*r1*r1;
    double ang1=acos((r1*r1+d*d-r2*r2)/(*r1*d));
    double ang2=acos((r2*r2+d*d-r1*r1)/(*r2*d));
    return ang1*r1*r1 + ang2*r2*r2 - r1*d*sin(ang1);
}
int main()
{
    int T,cas=;
    scanf("%d",&T);
    while(T--)
    {
        double r1,r2;
        Point a,b;
        scanf("%lf%lf%lf%lf%lf%lf",&r1,&r2,&a.x,&a.y,&b.x,&b.y);
        printf("Case #%d: %.6f\n",cas++,AREA(a,r2,b,r2)-AREA(a,r1,b,r2)-AREA(a,r2,b,r1)+AREA(a,r1,b,r1));
    }
    return ;
}