FJNU2018低程A 逃跑路线（Lucas + 中国剩余定理 + LGV定理）题解

题目描述

n个人在w*h的监狱里面想要逃跑,已知他们的同伙在坐标(bi,h)接应他们,他们现在被关在(ai,1)现在他们必须要到同伙那里才有逃出去的机会,这n个人又很蠢只会从(x,y)->(x+1,y),(x,y+1)并且这他们走过的路径不能相交如果相交第一个经过后就会有第二个人经过时候就会有一名狱警在那等他,第二个人就会被抓,假设他们不会同时踩到某个格子，那么他们的逃跑路线有多少不同的方案数。如果两个方案不同那么存在一个人踩的格子至少有一个是另外一个方案的没踩过

输入

第一行一个t(t<=20)表示测试样例 
第二行两个3个正整数n,w,h(n<=100,w,h<=1e9) 
接下来n行每行两个整数 
ai,bi(ai,bi<=w) 

输出

输出一个整数表示答案最终结果取膜109*1000003

样例输入

1
2 4 2
1 2
3 4

样例输出

4

思路：

这里有一个结论，n个起点到n个终点的不相交路径的种数为：每个起点到每个终点的可能数组成的n*n的矩阵的行列式。

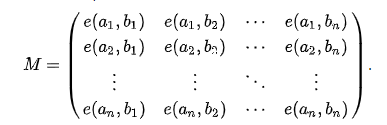
即求上矩阵行列式，其中e（ai，bi）代表从ai起点到bi终点的可能路径数量，行列式求解用高斯消元。

显然现在的问题是求解e。显然e（a[i],b[j]）= (h - 1 + b[j] - a[i], b[j] - a[i])或者0。

但是a、b、h范围均为1e9，那么求解组合数需要用到Lucas定理，但是mod = 109 * 1000003，显然是个合数，那么需要先质因数分解（显然分好了），然后中国剩余定理合并。

参考：

HDU 5852：Intersection is not allowed!（行列式+逆元求组合数）

hdu 5446 Unknown Treasure（Lucas定理+中国剩余定理）

Update：被工程卡时间卡的的心态崩了，优化了一些地方：

ll w = M / m[i];
d = exgcd(m[i], w, x, y);
ret = (ret + modmul(modmul(y, w, M), a[i], M) ) % M;

这里很显然不用每次都求w的逆元，因为w确定m[i]确定，直接小费马求出来保存就行。

还有很多取模都可以去掉，因为不论是阶乘还是阶乘的逆元，我们打表的时候都是%1e6+3，也就是说（1e6+3）^3也就18位左右，long long最大19位，似乎可以去掉（雾...

然后一些开long long开成int，就能慢慢卡进1000ms了（逃

admin标程跑的速度比我快了3倍...不知道什么操作

代码（新）：

#include<set>
#include<map>
#include<stack>
#include<cmath>
#include<queue>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
typedef long long ll;
using namespace std;
const int maxn = 1e5 + ;
const int seed = ;
const ll MOD =  * ;
const int INF = 0x3f3f3f3f;
int a[], b[];
ll e[][];
ll fac[][], inv[][];
ll modmul(ll a, ll b, ll p){
    ll ret = ;
    while(b) {
        if(b & ) ret = ret + a;
        if(ret >= p) ret -= p;
        a <<= ;
        if(a >= p) a -= p;
        b >>= ;
    }
    return ret;
}
ll pmul(ll a, ll b, ll p){
    ll ans = ;
    a %= p;
    while(b){
        if(b & ) ans = ans * a % p;
        a = a * a % p;
        b >>= ;
    }
    return ans;
}
ll C(ll n, ll m, ll p, int i){
    if(m > n) return ;
    return fac[i][n] * inv[i][m] * inv[i][n - m] % p;
}
ll Lucas(ll n, ll m, ll p, int i){
    if(m == ) return ;
    if(n < p && m < p) return C(n, m, p, i);
    return C(n % p, m % p, p, i) * Lucas(n / p, m / p, p, i) % p;
}
ll mm[] = {, };
ll remainder(ll a[], ll m[], int len){
    ll x, y, ret = ;
    ll M = MOD;
    for (int i = ; i < len; i++){
        ll w = M / m[i];
        ret = (ret + a[i] * mm[i] * w) % M;
    }
    return ret;
}
ll guass(int n, ll p){
    ll ans = , f = ;
    for(int i = ; i <= n; i++){
        for(int j = i + ; j <= n; j++){
            int x = i, y = j;
            while(e[y][i]){
                ll t = e[x][i] / e[y][i];
                for(int k = i; k <= n; k++)
                    e[x][k] = (e[x][k] - e[y][k] * t % p) % p;
                swap(x,y);
            }
            if(x != i){
                for(int k = ; k <= n; k++)
                    swap(e[i][k], e[j][k]);
                f = -f;
            }
        }
        ans = ans * e[i][i] % p;
        if(ans == ) return ;
    }
    return (ans * f + p) % p;
}
void init(int x, int n){
    fac[x][] = ;
    for (ll i = ; i < n; i++) fac[x][i] = fac[x][i - ] * i % n;
    inv[x][n - ] = pmul(fac[x][n - ], n - , n);
    for (ll i = n - ; i >= ; i--) inv[x][i] = inv[x][i + ] * (i + ) % n;
}
ll lucas[];
ll pp[] = {, };
ll solve(ll n, ll m){
    ll ret;
    for(int i = ; i < ; i++){
        lucas[i] = Lucas(n, m, pp[i], i);
    }
    ret = remainder(lucas, pp, );
    return ret;
}
int main(){
    init(, );
    init(, );
    int t;
    scanf("%d", &t);
    while(t--){
        ll n, w, h;
        scanf("%lld%lld%lld", &n, &w, &h);
        for(int i = ; i <= n; i++)
            scanf("%d%d", &a[i], &b[i]);
        for(int i = ; i <= n; i++){
            for(int j = ; j <= n; j++){
                if(b[j] >= a[i]){
                    e[i][j] = solve(h -  + b[j] - a[i], b[j] - a[i]);
                }
                else e[i][j] = ;
            }
        }
        printf("%lld\n", guass(n, MOD));
    }
    return ;
}

代码：

#include<set>
#include<map>
#include<stack>
#include<cmath>
#include<queue>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
typedef long long ll;
using namespace std;
const int maxn = 1e5 + ;
const int seed = ;
const ll MOD =  * ;
const int INF = 0x3f3f3f3f;
ll a[maxn], b[maxn];
ll e[][];
ll prime[maxn], p[maxn], pn;
ll fac[][];
ll pmul(ll a, ll b, ll p){
    ll ans = ;
    while(b){
        if(b & ) ans = ans * a % p;
        a = a * a % p;
        b >>= ;
    }
    return ans;
}
ll modmul(ll a, ll b, ll p) {
    ll ret = ;
    while(b) {
        if(b & ) ret = (ret + a) % p;
        a = (a + a) % p;
        b >>= ;
    }
    return ret;
}
ll Lucas(ll n, ll m, ll p, int i) {
    ll ret=;
    while(n && m) {
        ll a = n%p, b = m%p;
        if(a<b) return ;
        ret = (ret * fac[i][a] * pmul(fac[i][b]*fac[i][a - b] % p, p-, p)) % p;
        n/=p;
        m/=p;
    }
    return ret;
}

ll exgcd (ll a, ll b, ll &x, ll &y) {
    if (!b) {
        x = , y = ;
        return a;
    }
    int ans = exgcd ( b , a % b , y , x );
    y -= a / b * x;
    return ans;
}
ll remainder(ll a[], ll m[], int len) {
    ll d, x, y, ret = ;
    ll M = ;
    for (int i = ; i < len; i++) M *= m[i];
    for (int i = ; i < len; i++) {
        ll w = M / m[i];
        d = exgcd(m[i], w, x, y);
        ret = (ret + modmul(modmul(y, w, M), a[i], M) ) % M;
    }
    return (ret + M) % M;
}
ll guass(int n, ll MOD){
    ll ans = , f = ;
    for(int i = ; i <= n; i++){
        for(int j = i + ; j <= n; j++){
            int x = i, y = j;
            while(e[y][i]){
                ll t = e[x][i] / e[y][i];
                for(int k = i; k <= n; k++)
                    e[x][k] = (e[x][k] - e[y][k] * 1LL * t % MOD) % MOD;
                swap(x,y);
            }
            if(x != i){
                for(int k = ; k <= n; k++)
                    swap(e[i][k], e[j][k]);
                f = -f;
            }
        }
        ans = ans * e[i][i] % MOD;
        if(ans == ) return ;
    }
    return (ans * f + MOD) % MOD;
}
void init(){
    memset(prime, , sizeof(prime));
    pn = ;
    for(ll i = ; i < maxn; i++){
        if(!prime[i]){
            p[pn++] = i;
            for(ll j = i * i; j < maxn; j += i)
                prime[i] = ;
        }
    }
    fac[][] = ;
    for(int i = ; i <= ; i++){
        fac[][i] = (fac[][i-]*i) % ;
    }
    fac[][] = ;
    for(ll i = ; i <= ; i++){
        fac[][i] = (fac[][i-]*i) % ;
    }
}
ll solve(ll n, ll m){
    ll ret;
    ll lucas[];
    ll p[] = {, };
    for(int i = ; i < ; i++){
        lucas[i] = Lucas(n, m, p[i], i);
    }
    return ret = remainder(lucas, p, );
}
int main(){
    init();
    int t;
    scanf("%d", &t);
    while(t--){
        ll n, w, h;
        scanf("%lld%lld%lld", &n, &w, &h);
        for(int i = ; i <= n; i++)
            scanf("%lld%lld", &a[i], &b[i]);
        for(int i = ; i <= n; i++){
            for(int j = ; j <= n; j++){
                if(b[j] >= a[i]){
                    e[i][j] = solve(h -  + b[j] - a[i], b[j] - a[i]);
                }
                else e[i][j] = ;
            }
        }
        printf("%lld\n", guass(n, MOD));
    }
    return ;
}