ZOJ 3640 Help Me Escape：期望dp

题目链接：http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3640

题意：

　　有一个吸血鬼被困住了，他要逃跑。。。

　　他面前有n条路，每条路有一个困难程度c[i]。

　　他的初始攻击力为f。

　　每天他会从中随机选一条路：

　　　　（1）如果当前攻击力 > c[i]，那么他会再花t天走这条路成功逃跑（t的公式如图）。

　　　　　　

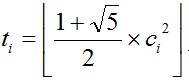
　　　　（2）攻击力 <= c[i]，这条路他走不过去，但可以让他的攻击力 += c[i]。

　　问你成功逃跑所需天数的期望。

题解：

　　表示状态：

　　　　dp[i] = expected time（攻击力为i时，逃跑还需要的天数）

　　找出答案：

　　　　ans = dp[f]

　　　　初始攻击力为f。

　　如何转移：

　　　　对于每一条路，每一次被选择的概率都为1/n。

　　　　当前攻击力为i，枚举每一条路j，则：

　　　　　　（1）if i > c[j]: dp[i] += t/n　（可以用t天逃跑）

　　　　　　（2）else: dp[i] += (dp[i+c[j]]+1)/n　（攻击力增加c[j]后所用天数 + 今天一天）

　　边界条件：

　　　　对于一个攻击力max_atk满足max_atk > 所有的c[i]，则所有的dp[max_atk]都相等。

　　　　（因为只能逃跑，不能再攒攻击力了）

　　　　所以找出满足条件的最小的max_atk，max_atk = max( max(c[i]), f )。

　　　　可能用到的攻击力最大为max_atk*2。

　　　　（根据Code: "else dp[i]+=(dp[i+c[j]]+1)/n"）

　　　　所以按从max_atk*2到f的顺序求dp就行了。

　　　　初始值（设成啥都行。。。没用）：set dp = 0

AC Code:

 // state expression:
 // dp[i] = expected time
 // i: present atk
 //
 // find the answer:
 // ans = dp[f]
 //
 // transferring:
 // now: dp[i]
 // enum: c[j]
 // if i > c[j] dp[i] += t/n
 // else dp[i] += (dp[i+c[j]]+1)/n
 //
 // boundary:
 // set dp = 0
 #include <iostream>
 #include <stdio.h>
 #include <string.h>
 #include <math.h>
 #define MAX_N 105
 #define MAX_F 30005

 using namespace std;

 int n,f;
 int max_atk;
 int c[MAX_N];
 double dp[MAX_F];

 void read()
 {
     max_atk=f;
     for(int i=;i<n;i++)
     {
         cin>>c[i];
         max_atk=max(max_atk,c[i]);
     }
 }

 void solve()
 {
     memset(dp,,sizeof(dp));
     for(int i=max_atk*+;i>=f;i--)
     {
         for(int j=;j<n;j++)
         {
             if(i>c[j]) dp[i]+=floor((1.0+sqrt())/2.0*c[j]*c[j])/n;
             else dp[i]+=(dp[i+c[j]]+)/n;
         }
     }
 }

 void print()
 {
     printf("%.3f\n",dp[f]);
 }

 int main()
 {
     while(cin>>n>>f)
     {
         read();
         solve();
         print();
     }
 }