TensorFlow中设置学习率的方式
上文深度神经网络中各种优化算法原理及比较中介绍了深度学习中常见的梯度下降优化算法;其中,有一个重要的超参数——学习率\(\alpha\)需要在训练之前指定,学习率设定的重要性不言而喻:过小的学习率会降低网络优化的速度,增加训练时间;而过大的学习率则可能导致最后的结果不会收敛,或者在一个较大的范围内摆动;因此,在训练的过程中,根据训练的迭代次数调整学习率的大小,是非常有必要的;
因此,本文主要介绍TensorFlow中如何使用学习率、TensorFlow中的几种学习率设置方式;文章中参考引用文献将不再具体文中说明,在文章末尾处会给出所有的引用文献链接;
本主要主要介绍的学习率设置方式有:
- 指数衰减: tf.train.exponential_decay()
- 分段常数衰减: tf.train.piecewise_constant()
- 自然指数衰减: tf.train.natural_exp_decay()
- 多项式衰减tf.train.polynomial_decay()
- 倒数衰减tf.train.inverse_time_decay()
- 余弦衰减tf.train.cosine_decay()
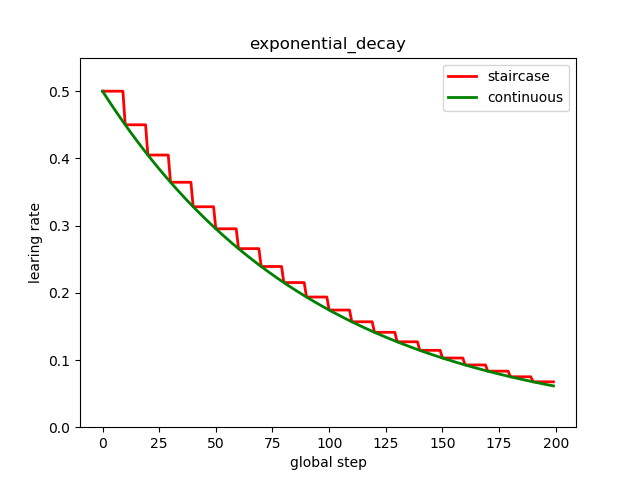
1. 指数衰减
tf.train.exponential_decay(
learning_rate,
global_step,
decay_steps,
decay_rate,
staircase=False,
name=None):
| 参数 | 用法 |
|---|---|
learning_rate |
初始学习率; |
global_step |
迭代次数; |
decay_steps |
衰减周期,当staircase=True时,学习率在\(decay\_steps\)内保持不变,即得到离散型学习率; |
decay_rate |
衰减率系数; |
staircase |
是否定义为离散型学习率,默认False; |
name |
名称,默认ExponentialDecay; |
计算方式:
decayed_learning_rate = learning_rate * decay_rate ^ (global_step / decay_steps)
# 如果staircase=True,则学习率会在得到离散值,每decay_steps迭代次数,更新一次;
示例:
# coding:utf-8
import matplotlib.pyplot as plt
import tensorflow as tf
global_step = tf.Variable(0, name='global_step', trainable=False) # 迭代次数
y = []
z = []
EPOCH = 200
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for global_step in range(EPOCH):
# 阶梯型衰减
learing_rate1 = tf.train.exponential_decay(
learning_rate=0.5, global_step=global_step, decay_steps=10, decay_rate=0.9, staircase=True)
# 标准指数型衰减
learing_rate2 = tf.train.exponential_decay(
learning_rate=0.5, global_step=global_step, decay_steps=10, decay_rate=0.9, staircase=False)
lr1 = sess.run([learing_rate1])
lr2 = sess.run([learing_rate2])
y.append(lr1)
z.append(lr2)
x = range(EPOCH)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_ylim([0, 0.55])
plt.plot(x, y, 'r-', linewidth=2)
plt.plot(x, z, 'g-', linewidth=2)
plt.title('exponential_decay')
ax.set_xlabel('step')
ax.set_ylabel('learing rate')
plt.legend(labels = ['staircase', 'continus'], loc = 'upper right')
plt.show()
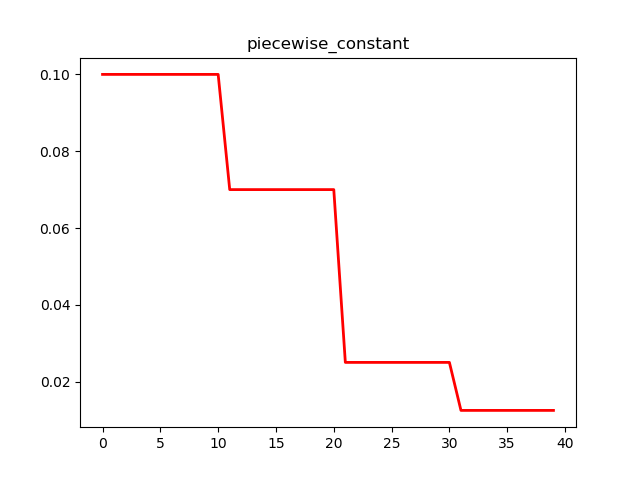
2. 分段常数衰减
tf.train.piecewise_constant(
x,
boundaries,
values,
name=None):
| 参数 | 用法 |
|---|---|
x |
相当于global_step,迭代次数; |
boundaries |
列表,表示分割的边界; |
values |
列表,分段学习率的取值; |
name |
名称,默认PiecewiseConstant; |
计算方式:
# parameter
global_step = tf.Variable(0, trainable=False)
boundaries = [100, 200]
values = [1.0, 0.5, 0.1]
# learning_rate
learning_rate = tf.train.piecewise_constant(global_step, boundaries, values)
# 解释
# 当global_step=[1, 100]时,learning_rate=1.0;
# 当global_step=[101, 200]时,learning_rate=0.5;
# 当global_step=[201, ~]时,learning_rate=0.1;
示例:
# coding:utf-8
import matplotlib.pyplot as plt
import tensorflow as tf
global_step = tf.Variable(0, name='global_step', trainable=False)
boundaries = [10, 20, 30]
learing_rates = [0.1, 0.07, 0.025, 0.0125]
y = []
N = 40
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for global_step in range(N):
learing_rate = tf.train.piecewise_constant(global_step, boundaries=boundaries, values=learing_rates)
lr = sess.run([learing_rate])
y.append(lr)
x = range(N)
plt.plot(x, y, 'r-', linewidth=2)
plt.title('piecewise_constant')
plt.show()
3. 自然指数衰减
类似与指数衰减,同样与当前迭代次数相关,只不过以e为底;
tf.train.natural_exp_decay(
learning_rate,
global_step,
decay_steps,
decay_rate,
staircase=False,
name=None
)
| 参数 | 用法 |
|---|---|
learning_rate |
初始学习率; |
global_step |
迭代次数; |
decay_steps |
衰减周期,当staircase=True时,学习率在\(decay\_steps\)内保持不变,即得到离散型学习率; |
decay_rate |
衰减率系数; |
staircase |
是否定义为离散型学习率,默认False; |
name |
名称,默认ExponentialTimeDecay; |
计算方式:
decayed_learning_rate = learning_rate * exp(-decay_rate * global_step)
# 如果staircase=True,则学习率会在得到离散值,每decay_steps迭代次数,更新一次;
示例:
# coding:utf-8
import matplotlib.pyplot as plt
import tensorflow as tf
global_step = tf.Variable(0, name='global_step', trainable=False)
y = []
z = []
w = []
m = []
EPOCH = 200
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for global_step in range(EPOCH):
# 阶梯型衰减
learing_rate1 = tf.train.natural_exp_decay(
learning_rate=0.5, global_step=global_step, decay_steps=10, decay_rate=0.9, staircase=True)
# 标准指数型衰减
learing_rate2 = tf.train.natural_exp_decay(
learning_rate=0.5, global_step=global_step, decay_steps=10, decay_rate=0.9, staircase=False)
# 阶梯型指数衰减
learing_rate3 = tf.train.exponential_decay(
learning_rate=0.5, global_step=global_step, decay_steps=10, decay_rate=0.9, staircase=True)
# 标准指数衰减
learing_rate4 = tf.train.exponential_decay(
learning_rate=0.5, global_step=global_step, decay_steps=10, decay_rate=0.9, staircase=False)
lr1 = sess.run([learing_rate1])
lr2 = sess.run([learing_rate2])
lr3 = sess.run([learing_rate3])
lr4 = sess.run([learing_rate4])
y.append(lr1)
z.append(lr2)
w.append(lr3)
m.append(lr4)
x = range(EPOCH)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_ylim([0, 0.55])
plt.plot(x, y, 'r-', linewidth=2)
plt.plot(x, z, 'g-', linewidth=2)
plt.plot(x, w, 'r--', linewidth=2)
plt.plot(x, m, 'g--', linewidth=2)
plt.title('natural_exp_decay')
ax.set_xlabel('step')
ax.set_ylabel('learing rate')
plt.legend(labels = ['natural_staircase', 'natural_continus', 'staircase', 'continus'], loc = 'upper right')
plt.show()
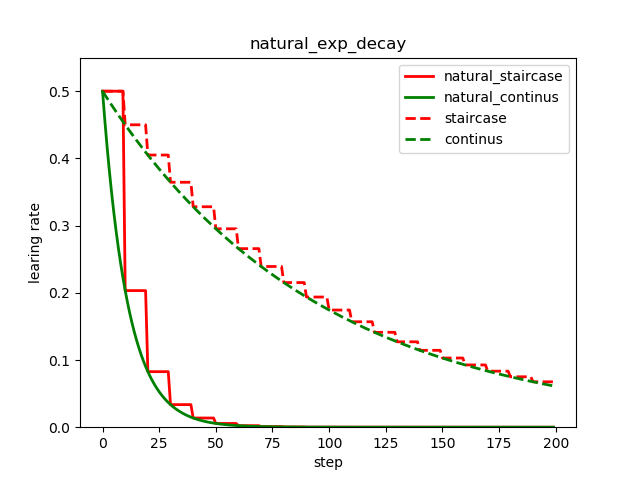
可以看到自然指数衰减对学习率的衰减程度远大于一般的指数衰减;
4. 多项式衰减
tf.train.polynomial_decay(
learning_rate,
global_step,
decay_steps,
end_learning_rate=0.0001,
power=1.0,
cycle=False, name=None):
| 参数 | 用法 |
|---|---|
learning_rate |
初始学习率; |
global_step |
迭代次数; |
decay_steps |
衰减周期; |
end_learning_rate |
最小学习率,默认0.0001; |
power |
多项式的幂,默认1; |
cycle |
bool,表示达到最低学习率时,是否升高再降低,默认False; |
name |
名称,默认PolynomialDecay; |
计算方式:
# 如果cycle=False
global_step = min(global_step, decay_steps)
decayed_learning_rate = (learning_rate - end_learning_rate) *
(1 - global_step / decay_steps) ^ (power) +
end_learning_rate
# 如果cycle=True
decay_steps = decay_steps * ceil(global_step / decay_steps)
decayed_learning_rate = (learning_rate - end_learning_rate) *
(1 - global_step / decay_steps) ^ (power) +
end_learning_rate
示例:
# coding:utf-8
import matplotlib.pyplot as plt
import tensorflow as tf
y = []
z = []
EPOCH = 200
global_step = tf.Variable(0, name='global_step', trainable=False)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for global_step in range(EPOCH):
# cycle=False
learing_rate1 = tf.train.polynomial_decay(
learning_rate=0.1, global_step=global_step, decay_steps=50,
end_learning_rate=0.01, power=0.5, cycle=False)
# cycle=True
learing_rate2 = tf.train.polynomial_decay(
learning_rate=0.1, global_step=global_step, decay_steps=50,
end_learning_rate=0.01, power=0.5, cycle=True)
lr1 = sess.run([learing_rate1])
lr2 = sess.run([learing_rate2])
y.append(lr1)
z.append(lr2)
x = range(EPOCH)
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(x, z, 'g-', linewidth=2)
plt.plot(x, y, 'r--', linewidth=2)
plt.title('polynomial_decay')
ax.set_xlabel('step')
ax.set_ylabel('learing rate')
plt.legend(labels=['cycle=True', 'cycle=False'], loc='uppper right')
plt.show()
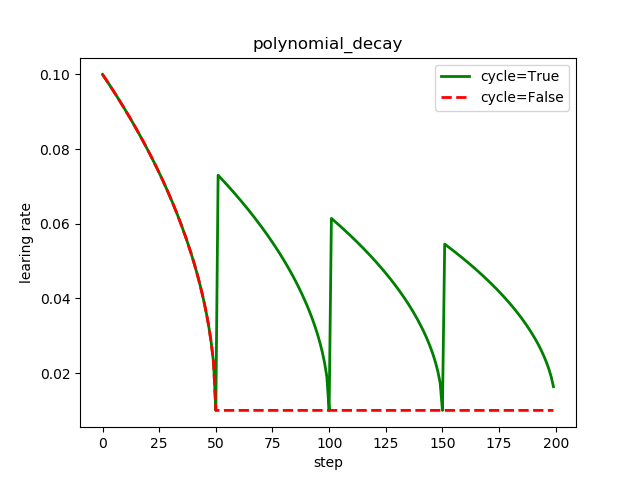
可以看到学习率在decay_steps=50迭代次数后到达最小值;同时,当cycle=False时,学习率达到预设的最小值后,就保持最小值不再变化;当cycle=True时,学习率将会瞬间增大,再降低;
多项式衰减中设置学习率可以往复升降的目的:时为了防止在神经网络训练后期由于学习率过小,导致网络参数陷入局部最优,将学习率升高,有可能使其跳出局部最优;
5. 倒数衰减
inverse_time_decay(
learning_rate,
global_step,
decay_steps,
decay_rate,
staircase=False,
name=None):
| 参数 | 用法 |
|---|---|
learning_rate |
初始学习率; |
global_step |
迭代次数; |
decay_steps |
衰减周期; |
decay_rate |
学习率衰减参数; |
staircase |
是否得到离散型学习率,默认False; |
name |
名称;默认InverseTimeDecay; |
计算方式:
# 如果staircase=False,即得到连续型衰减学习率;
decayed_learning_rate = learning_rate / (1 + decay_rate * global_step / decay_step)
# 如果staircase=True,即得到离散型衰减学习率;
decayed_learning_rate = learning_rate / (1 + decay_rate * floor(global_step / decay_step))
示例:
# coding:utf-8
import matplotlib.pyplot as plt
import tensorflow as tf
y = []
z = []
EPOCH = 200
global_step = tf.Variable(0, name='global_step', trainable=False)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for global_step in range(EPOCH):
# 阶梯型衰减
learing_rate1 = tf.train.inverse_time_decay(
learning_rate=0.1, global_step=global_step, decay_steps=20,
decay_rate=0.2, staircase=True)
# 连续型衰减
learing_rate2 = tf.train.inverse_time_decay(
learning_rate=0.1, global_step=global_step, decay_steps=20,
decay_rate=0.2, staircase=False)
lr1 = sess.run([learing_rate1])
lr2 = sess.run([learing_rate2])
y.append(lr1)
z.append(lr2)
x = range(EPOCH)
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(x, z, 'r-', linewidth=2)
plt.plot(x, y, 'g-', linewidth=2)
plt.title('inverse_time_decay')
ax.set_xlabel('step')
ax.set_ylabel('learing rate')
plt.legend(labels=['continus', 'staircase'])
plt.show()
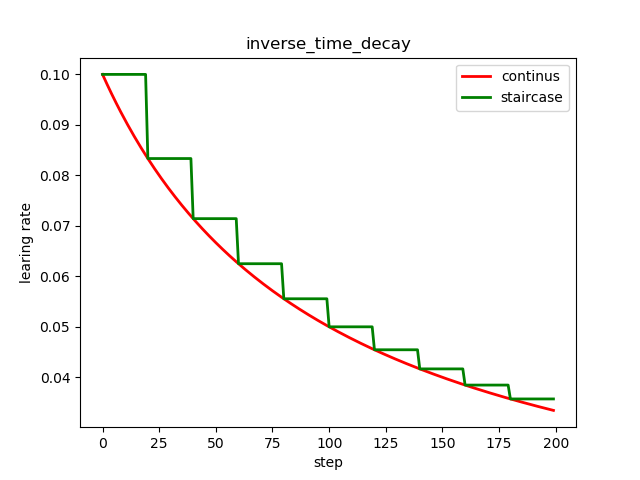
同样可以看到,随着迭代次数的增加,学习率在逐渐减小,同时减小的幅度也在降低;
6. 余弦衰减
之前使用TensorFlow的版本是1.4,没有学习率的余弦衰减;之后升级到了1.9版本,发现多了四个有关学习率余弦衰减的方法;下面将进行介绍:
6.1 标准余弦衰减
来源于:[Loshchilov & Hutter, ICLR2016], SGDR: Stochastic Gradient Descent with Warm Restarts. https://arxiv.org/abs/1608.03983
tf.train.cosine_decay(
learning_rate,
global_step,
decay_steps,
alpha=0.0,
name=None):
| 参数 | 用法 |
|---|---|
learning_rate |
初始学习率; |
global_step |
迭代次数; |
decay_steps |
衰减周期; |
alpha |
最小学习率,默认为0; |
name |
名称,默认CosineDecay; |
计算方式:
global_step = min(global_step, decay_steps)
cosine_decay = 0.5 * (1 + cos(pi * global_step / decay_steps))
decayed = (1 - alpha) * cosine_decay + alpha
decayed_learning_rate = learning_rate * decayed
示例:
# coding:utf-8
import matplotlib.pyplot as plt
import tensorflow as tf
y = []
z = []
EPOCH = 200
global_step = tf.Variable(0, name='global_step', trainable=False)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for global_step in range(EPOCH):
# 余弦衰减
learing_rate1 = tf.train.cosine_decay(
learning_rate=0.1, global_step=global_step, decay_steps=50)
learing_rate2 = tf.train.cosine_decay(
learning_rate=0.1, global_step=global_step, decay_steps=100)
lr1 = sess.run([learing_rate1])
lr2 = sess.run([learing_rate2])
y.append(lr1)
z.append(lr2)
x = range(EPOCH)
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(x, y, 'r-', linewidth=2)
plt.plot(x, z, 'b-', linewidth=2)
plt.title('cosine_decay')
ax.set_xlabel('step')
ax.set_ylabel('learing rate')
plt.legend(labels=['decay_steps=50', 'decay_steps=100'],z loc='upper right')
plt.show()
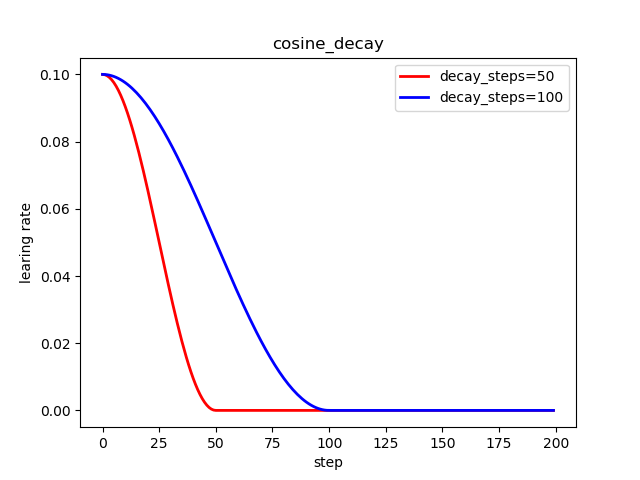
6.2 重启余弦衰减
来源于:[Loshchilov & Hutter, ICLR2016], SGDR: Stochastic Gradient Descent with Warm Restarts. https://arxiv.org/abs/1608.03983
tf.train.cosine_decay_restarts(
learning_rate,
global_step,
first_decay_steps,
t_mul=2.0,
m_mul=1.0,
alpha=0.0,
name=None):
| 参数 | 用法 |
|---|---|
learning_rate |
初始学习率; |
global_step |
迭代次数; |
first_decay_steps |
衰减周期; |
t_mul |
Used to derive the number of iterations in the i-th period |
m_mul |
Used to derive the initial learning rate of the i-th period: |
alpha |
最小学习率,默认为0; |
name |
名称,默认SGDRDecay; |
示例:
# coding:utf-8
import matplotlib.pyplot as plt
import tensorflow as tf
y = []
z = []
EPOCH = 100
global_step = tf.Variable(0, name='global_step', trainable=False)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for global_step in range(EPOCH):
# 重启余弦衰减
learing_rate1 = tf.train.cosine_decay_restarts(learning_rate=0.1, global_step=global_step,
first_decay_steps=40)
learing_rate2 = tf.train.cosine_decay_restarts(learning_rate=0.1, global_step=global_step,
first_decay_steps=60)
lr1 = sess.run([learing_rate1])
lr2 = sess.run([learing_rate2])
y.append(lr1)
z.append(lr2)
x = range(EPOCH)
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(x, y, 'r-', linewidth=2)
plt.plot(x, z, 'b-', linewidth=2)
plt.title('cosine_decay')
ax.set_xlabel('step')
ax.set_ylabel('learing rate')
plt.legend(labels=['decay_steps=40', 'decay_steps=60'], loc='upper right')
plt.show()
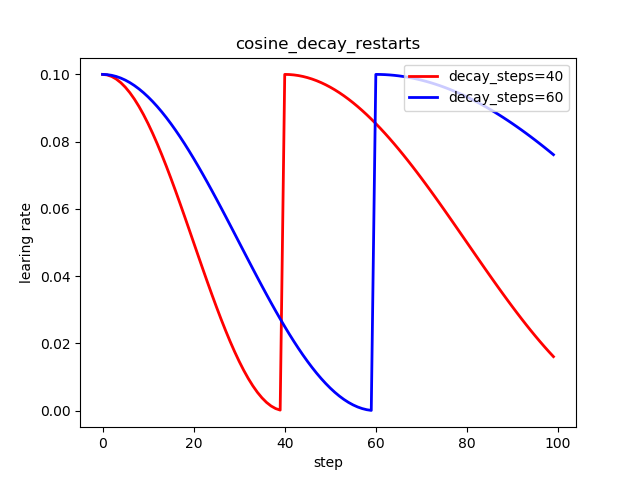
6.3 线性余弦噪声
来源于:[Bello et al., ICML2017] Neural Optimizer Search with RL. https://arxiv.org/abs/1709.07417
tf.train.linear_cosine_decay(
learning_rate,
global_step,
decay_steps,
num_periods=0.5,
alpha=0.0,
beta=0.001,
name=None):
| 参数 | 用法 |
|---|---|
learning_rate |
初始学习率; |
global_step |
迭代次数; |
decay_steps |
衰减周期; |
num_periods |
Number of periods in the cosine part of the decay. |
alpha |
最小学习率; |
beta |
同上; |
name |
名称, |
计算方式:
global_step = min(global_step, decay_steps)
linear_decay = (decay_steps - global_step) / decay_steps)
cosine_decay = 0.5 * (1 + cos(pi * 2 * num_periods * global_step / decay_steps))
decayed = (alpha + linear_decay) * cosine_decay + beta
decayed_learning_rate = learning_rate * decayed
示例:
# coding:utf-8
import matplotlib.pyplot as plt
import tensorflow as tf
y = []
z = []
EPOCH = 100
global_step = tf.Variable(0, name='global_step', trainable=False)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for global_step in range(EPOCH):
# 线性余弦衰减
learing_rate1 = tf.train.linear_cosine_decay(
learning_rate=0.1, global_step=global_step, decay_steps=40,
num_periods=0.2, alpha=0.5, beta=0.2)
learing_rate2 = tf.train.linear_cosine_decay(
learning_rate=0.1, global_step=global_step, decay_steps=60,
num_periods=0.2, alpha=0.5, beta=0.2)
lr1 = sess.run([learing_rate1])
lr2 = sess.run([learing_rate2])
y.append(lr1)
z.append(lr2)
x = range(EPOCH)
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(x, y, 'r-', linewidth=2)
plt.plot(x, z, 'b-', linewidth=2)
plt.title('linear_cosine_decay')
ax.set_xlabel('step')
ax.set_ylabel('learing rate')
plt.legend(labels=['decay_steps=40', 'decay_steps=60'], loc='upper right')
plt.show()
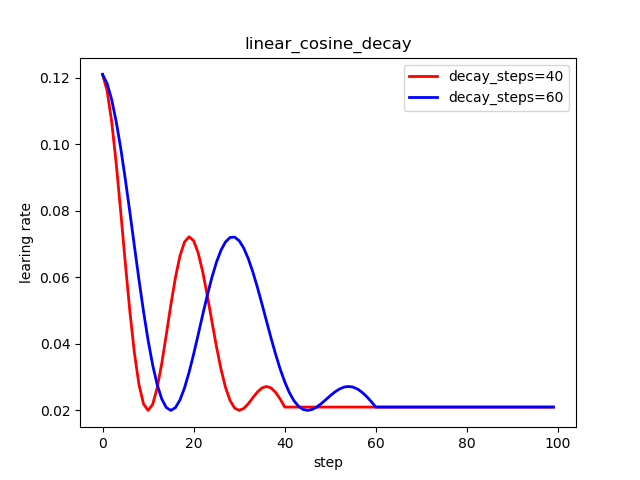
6.4 噪声余弦衰减
来源于:[Bello et al., ICML2017] Neural Optimizer Search with RL. https://arxiv.org/abs/1709.07417
tf.train.noisy_linear_cosine_decay(
learning_rate,
global_step,
decay_steps,
initial_variance=1.0,
variance_decay=0.55,
num_periods=0.5,
alpha=0.0,
beta=0.001,
name=None):
| 参数 | 用法 |
|---|---|
learning_rate |
初始学习率; |
global_step |
迭代次数; |
decay_steps |
衰减周期; |
initial_variance |
initial variance for the noise. |
variance_decay |
decay for the noise's variance. |
num_periods |
Number of periods in the cosine part of the decay. |
alpha |
最小学习率; |
beta |
查看计算公式; |
name |
名称,默认NoisyLinearCosineDecay; |
计算方式:
global_step = min(global_step, decay_steps)
linear_decay = (decay_steps - global_step) / decay_steps)
cosine_decay = 0.5 * (
1 + cos(pi * 2 * num_periods * global_step / decay_steps))
decayed = (alpha + linear_decay + eps_t) * cosine_decay + beta
decayed_learning_rate = learning_rate * decayed
示例:
# coding:utf-8
import matplotlib.pyplot as plt
import tensorflow as tf
y = []
z = []
EPOCH = 100
global_step = tf.Variable(0, name='global_step', trainable=False)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for global_step in range(EPOCH):
# # 噪声线性余弦衰减
learing_rate1 = tf.train.noisy_linear_cosine_decay(
learning_rate=0.1, global_step=global_step, decay_steps=40,
initial_variance=0.01, variance_decay=0.1, num_periods=2, alpha=0.5, beta=0.2)
learing_rate2 = tf.train.noisy_linear_cosine_decay(
learning_rate=0.1, global_step=global_step, decay_steps=60,
initial_variance=0.01, variance_decay=0.1, num_periods=2, alpha=0.5, beta=0.2)
lr1 = sess.run([learing_rate1])
lr2 = sess.run([learing_rate2])
y.append(lr1)
z.append(lr2)
x = range(EPOCH)
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(x, y, 'r-', linewidth=2)
plt.plot(x, z, 'b-', linewidth=2)
plt.title('noisy_linear_cosine_decay')
ax.set_xlabel('step')
ax.set_ylabel('learing rate')
plt.legend(labels=['decay_steps=40', 'decay_steps=60'], loc='upper right')
plt.show()
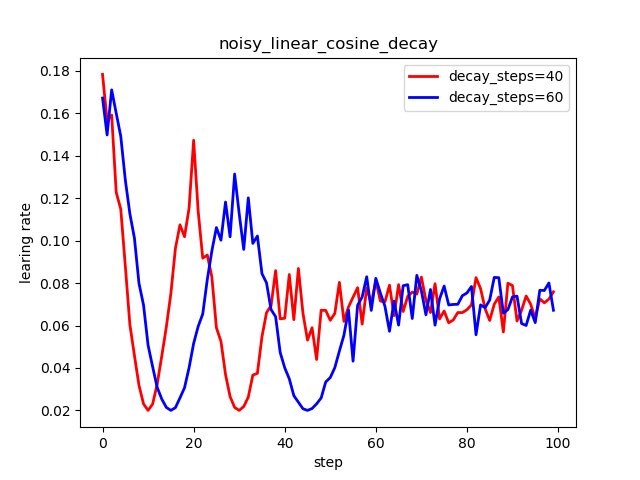
写在最后,将TensorFlow中提供的所有学习率衰减的方式大致地使用了一遍,突然发现,掌握的也仅仅是TensorFlow中提供了哪些衰减方式、大致如何使用;然而,当涉及到某种具体的衰减方式、参数如何设置与背后的数学意义,以及不同的方法适用于什么情况....等等一些问题,仍不能掌握。如有可能,在之后使用的过程中,当发现有新的理解,再回来补充。
如有错误,请不吝指正,谢谢。
这里感谢未雨愁眸-tensorflow中学习率更新策略的博文,本文主要参考该篇文章;当然在其他地方也有看到类似文章,至于说首发何人何处,却未从考证;
博主个人网站:https://chenzhen.onliine
Reference
TensorFlow中设置学习率的方式的更多相关文章
- tensorflow中常用学习率更新策略
神经网络训练过程中,根据每batch训练数据前向传播的结果,计算损失函数,再由损失函数根据梯度下降法更新每一个网络参数,在参数更新过程中使用到一个学习率(learning rate),用来定义每次参数 ...
- tensorflow中的学习率调整策略
通常为了模型能更好的收敛,随着训练的进行,希望能够减小学习率,以使得模型能够更好地收敛,找到loss最低的那个点. tensorflow中提供了多种学习率的调整方式.在https://www.tens ...
- Tensorflow中卷积的padding方式
根据tensorflow中的Conv2D函数,先定义几个基本符号: 输入矩阵W*W,这里只考虑输入宽高相等的情况,如果不相等,推导方法一样 filter矩阵F*F,卷积核 stride值S,步长 输出 ...
- C# Excel 中设置文字对齐方式、方向和换行
在Excel表格中输入文字时,我们常常需要调整文字对齐方式或者对文字进行换行.本文将介绍如何通过编程的方式设置文字对齐方式,改变文字方向以及对文字进行换行. //创建Workbook对象 Workbo ...
- Eclipse中设置JDK内存方式
(1) 打开Eclipse,双击Serveers进入到servers编辑画面 (2) 点击 Open launch configuration 选项 (3) 选项中找到Arguments 的选项卡(t ...
- Eclipse中设置编码的方式
如果要使插件开发应用能有更好的国际化支持,能够最大程度的支持中文输出,则最好使 Java文件使用UTF-8编码.然而,Eclipse工 作空间(workspace)的缺省字符编码是操作系统缺省的编码, ...
- html中设置浏览器解码方式
通过添加一行标签: <meta http-equiv="Content-Type" content="text/html; charset=utf-8"& ...
- 转:Eclipse中设置编码的方式
来源:http://blog.csdn.net/jianw2007/article/details/3930915 如果要使插件开发应用能有更好的国际化支持,能够最大程度的支持中文输出,则最好使 Ja ...
- ASP.NET Core MVC 中设置全局异常处理方式
在asp.net core mvc中,如果有未处理的异常发生后,会返回http500错误,对于最终用户来说,显然不是特别友好.那如何对于这些未处理的异常显示统一的错误提示页面呢? 在asp.net c ...
随机推荐
- css浏览器兼容问题集锦
表单按钮用input type=submit和a链接两者表现不一致的问题 表单的输入框.文本.验证码图片没有对齐 IE6/7中margin失效 IE6中margin双边距 1.问题: 表单按钮用inp ...
- Windows编程MessageBox函数
API: int MessageBox(HWND hWnd, LPCTSTRlpText, LPCTSTRlpCaption, UINTuType); MSDN描述: This function cr ...
- 校园网络 usaco
这道题和上一道[最受欢迎的牛]差不多,都是强连通分量的练习题: 第一问实际上就是问缩点后入度为0的点有多少,第二问就是问添加几条边能使缩点后的图变成强连通图: 第一问好做,第二问需要动下脑子,也不难: ...
- c语言学习的第12天
#include <stdio.h> int main(void) { int *p; int i=5; char ch='A'; p=&i; *p=99; printf(&quo ...
- python类初探
class human: is_alive=True is_man=True def __init__(self,age): print('this is __init__() method, whi ...
- TP框架入门基础
ThinkPHP目录: ThinkPHP主目录文件夹: Conf文件夹: Library文件夹: Library=>Think文件夹:
- Dat.gui 使用教程
官方站点:http://workshop.chromeexperiments.com/examples/gui/ Dat.gui 使用教程:Dat.gui 是一个 GUI 组件,他可以为你的 demo ...
- MySQL计算指标连续两月金额相比_20160929
在正常的业务逻辑中,对客户的分析是必须的也是最经常用到的,根据时间维度计算计算指标连续两月环比情况也是一道必须面对的题目. 国庆放假 先写代码 后面再拆分解释 SELECT a.*,b.年月 AS 上 ...
- BZOJ_4025_二分图_线段树按时间分治+并查集
BZOJ_4025_二分图_线段树按时间分治+并查集 Description 神犇有一个n个节点的图.因为神犇是神犇,所以在T时间内一些边会出现后消失.神犇要求出每一时间段内这个图是否是二分图.这么简 ...
- 【Lintcode】099.Reorder List
题目: Given a singly linked list L: L0 → L1 → … → Ln-1 → Ln reorder it to: L0 → Ln → L1 → Ln-1 → L2 → ...
