Mojette

Mojette Transform 是由Polytech Nantes的IRCCYyN实验室的Jeanpierre Guédon首先提出的一种离散的几何转换，它来源于Radon transform，是Radon transform的离散的更准确的表达。

Radon Transform：

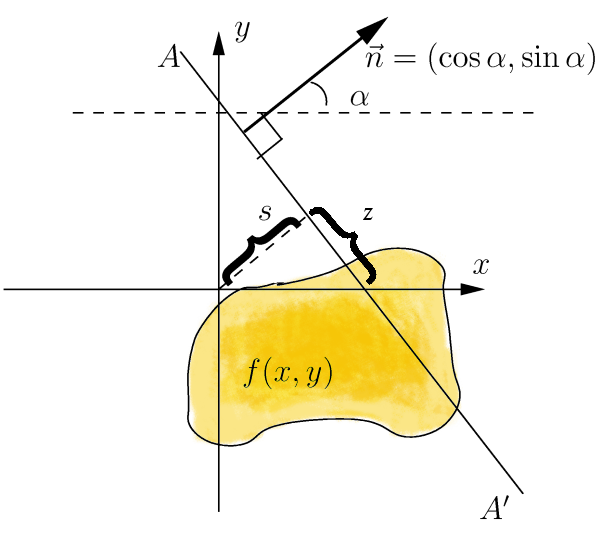
Radon transform 是将在一个坐标系中的几何形状以一定的角度映射到一个新的坐标上，如上图所示，在笛卡尔坐标系中的椭圆以角度θ映射到了一个新的坐标系中，其公式如下：

proj(t,θ)=∫∫f(x,y)δ(t-x.cosθ+y.sinθ)dxdy

符号δ表示面积相等

Mojette Transform：

Radon是连续的，Mojette则是离散的。

其转换公式为

proj(p,q,b)=∑∑f(k,l)Δ(b-pl+qk)

其中，q、p为投影的方向，k、l为坐标，b=pl-qk。 可以证明，在(p,q)方向上，共有nbins=(H-1)|q|+(W-1)|p|+1个新的坐标值（如上图，在4*4的矩形中，在(1,0)方向上有4个新的坐标值，在(1,1)方向上有7个新的坐标值）

任意大小的矩形的mojette变换的算法如下：

Begin

rectangle's height and width is H and W, the projection angle is p and q

nbins=(H-1)|q|+(W-1)|p|+1

//为了方便，我们从0开始计算的新的坐标值，即从0到nbins-1

//计算补偿值，每个坐标的投影后的新的坐标减去这个补偿值即可

HL=p(H-1)

HR=p(H-1)-q(W-1)

LR=-q(W-1)

LL=0

if HL<HR then offset=HL else offset=HR

if LR<offset then offset=LR

if LL<offset then offset=LL

//开始计算每个坐标对应的投影的值

for k=0:W-1

for l=0:H-1

b=pl-qk

proj(b-offset)+=f(k,l)

end for

end for

end

例：

如上图，假设为5*4的矩阵，横坐标k，纵坐标l，投影方向为(2,1)，首先对四个角计算其b值，将最小的设为offset，以(0,0)这一列为例计算其投影之后的值，在这一列上，共有(0,0),(2,1),(5,3)三个坐标，其b(b=pl-qk)值都为0，但是我们是从0开始索引，所以b-offset=4即为我们新的投影的坐标，而在新投影上的值为这三个值的和。

通过以上算法即可计算在任意大小的矩阵中任意投影方向的Mojette变换，但在实际应用中，反mojette变换才是最有用的，inverse-mojette将在下一篇博客中具体介绍。

如果有兴趣，可以登录http://www.mojette.net/ 查看关于Mojette的一个小游戏，其正是inverse-mojette变换的具体实例。