Solution -「LOCAL」「cov. HDU 6864」找朋友

\(\mathcal{Description}\)

  Link.（几乎一致）

  给定 \(n\) 个点 \(m\) 条边的仙人掌和起点 \(s\)，边长度均为 \(1\)。令 \(d(u)\) 表示 \(u\) 到 \(s\) 的最短距离。对于任意一个结点的排列 \(\{p_1,p_2,\cdots,p_n\}\)，记 \(t_i\) 满足 \(p_{t_i}=i\)，称排列合法，当且仅当：

\[(\forall(u,v)\in E)\left((d(u)<d(v)\rightarrow t_u<t_v)\land(d(u)>d(v)\rightarrow t_u>t_v)\right)
\]

  求合法排列数，对 \(998244353\) 取模。

  \(n\le10^4\)，\(m\le2\times10^4\)，保证不存在 \((u,v)\in E\)，使得 \(d(u)=d(v)\)。

\(\mathcal{Solution}\)

  考虑一个偶环（题目保证无奇环），起点终点在左右两端，上下各有 \(l\) 个结点相连。可见上下的点间是互不影响的，我们只需要分别保证上方和下方结点的相对位置。

  再考虑一棵树，每个结点必须先于其子树内的点出现，所有方案为 \(n!\)，每个结点 \(u\) 就会使其 \(\times\frac{1}{siz_u}\)。

  对于仙人掌，处理出一棵 BFS 树，并得到环的信息。对于非环上的点，直接按树上的点来贡献系数。否则，对于一个环，如图：

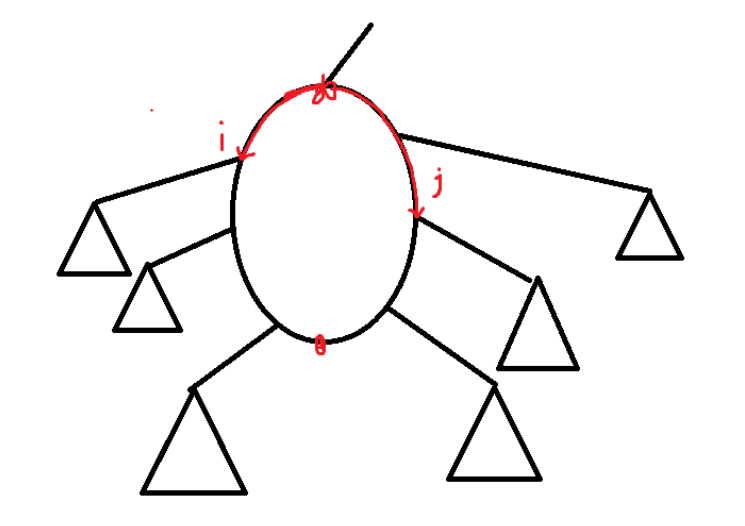
  DP 求解，当前子树顺序已确定，令 \(f(i,j)\) 表示用左边前 \(i\) 个和右边前 \(j\) 个时对答案贡献的系数。转移比较显：

\[f(i,j)=\frac{1}{siz_i+siz_j}(f(i-1,j)+f(i,j-1))
\]

  其中 \(siz_i\) 表示 \(i\) 在 BFS 树上的子树大小，需要特殊处理 \(i=0\) 或 \(j=0\) 的情况。

\(\mathcal{Code}\)

#include <queue>
#include <cstdio>
#include <vector>

typedef std::pair<int, int> pii;

const int MAXN = 1e4, MAXM = 2e4, MOD = 998244353;
int n, m, s, ecnt = 1, inv[MAXN + 5], head[MAXN + 5], dist[MAXN + 5];
int fa[MAXN + 5], siz[MAXN + 5], sL[MAXN + 5], sR[MAXN + 5], f[MAXN + 5][MAXN + 5];
bool cut[MAXM + 5], vis[MAXN + 5];
std::vector<pii> cir;

struct Edge { int to, nxt; } graph[MAXM * 2 + 5];

inline void link ( const int s, const int t ) {
	graph[++ ecnt] = { t, head[s] };
	head[s] = ecnt;
}

inline void initBFTree () {
	std::queue<int> que;
	que.push ( s ), dist[s] = 1;
	while ( !que.empty () ) {
		int u = que.front (); que.pop ();
		for ( int i = head[u], v; i; i = graph[i].nxt ) {
			if ( !dist[v = graph[i].to] ) {
				fa[v] = u, dist[v] = dist[u] + 1;
				que.push ( v );
			} else if ( dist[v] > dist[u] ) {
				cut[i >> 1] = true;
				cir.push_back ( pii ( u, v ) );
			}
		}
	}
}

inline void initSize ( const int u ) {
	siz[u] = 1;
	for ( int i = head[u], v; i; i = graph[i].nxt ) {
		if ( !cut[i >> 1] && ( v = graph[i].to ) ^ fa[u] ) {
			initSize ( v ), siz[u] += siz[v];
		}
	}
}

int main () {
	freopen ( "abgfriend.in", "r", stdin );
	freopen ( "abgfriend.out", "w", stdout );
	scanf ( "%d %d %d", &n, &m, &s );
	int ans = inv[1] = 1;
	for ( int i = 2; i <= n; ++ i ) {
		ans = 1ll * i * ans % MOD;
		inv[i] = 1ll * ( MOD - MOD / i ) * inv[MOD % i] % MOD;
	}
	for ( int i = 1, u, v; i <= m; ++ i ) {
		scanf ( "%d %d", &u, &v );
		link ( u, v ), link ( v, u );
	}
	initBFTree ();
	initSize ( s );
	for ( int i = 0; i ^ cir.size (); ++ i ) {
		int u = cir[i].first, v = cir[i].second, cnt = 0;
		for ( int p = u, q = fa[v]; p ^ q; p = fa[p], q = fa[q] ) {
			vis[p] = vis[q] = true, ++ cnt;
			sL[cnt] = siz[p], sR[cnt] = siz[q];
		}
		for ( int i = 0; i <= cnt; ++ i ) {
			for ( int j = 0; j <= cnt; ++ j ) {
				if ( !i && !j ) f[i][j] = 1;
				else if ( !i ) f[i][j] = 1ll * f[i][j - 1] * inv[sR[j]] % MOD;
				else if ( !j ) f[i][j] = 1ll * f[i - 1][j] * inv[sL[i] + siz[v]] % MOD;
				else f[i][j] = 1ll * ( f[i - 1][j] + f[i][j - 1] ) * inv[sL[i] + sR[j]] % MOD;
			}
		}
		ans = 1ll * ans * f[cnt][cnt] % MOD;
	}
	for ( int i = 1; i <= n; ++ i ) {
		if ( !vis[i] ) {
			ans = 1ll * ans * inv[siz[i]] % MOD;
		}
	}
	printf ( "%d\n", ans );
	return 0;
}

\(\mathcal{Details}\)

  一开始局部变量 cnt 没赋初值，Windows 贴心地帮助兔子清了零，然后在 Lemon 上测 RE 一大片 qwq……