OO第一单元作业—

简介

本单元作业分为三次

第一次作业:需要完成的任务为简单多项式导函数的求解。

第二次作业:需要完成的任务为包含简单幂函数和简单正余弦函数的导函数的求解。

第三次作业:需要完成的任务为包含简单幂函数和简单正余弦函数的导函数及其组合的求解。

第一次作业

实现方式

输入、解析：

1.
去掉所有空白符。

2.
经过一系列replaceAll使得项与项之间仅以+分隔。

3.
利用Split将所有项拆分开，对于每一个项新建一个对象。

求导：

1.
每个因子存储在Term中，调用求导方法进行求导并存入Hashmap。

输出：

1.
遍历Hashmap，正项先输出。

2.
指数为1和-1时采用省略模式输出。

3.
一开始不输出0项，如果到最后输出长度为0那么输出0。

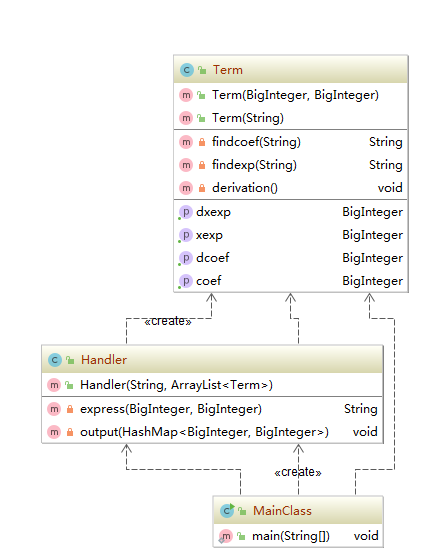
类图

代码规模

复杂度分析

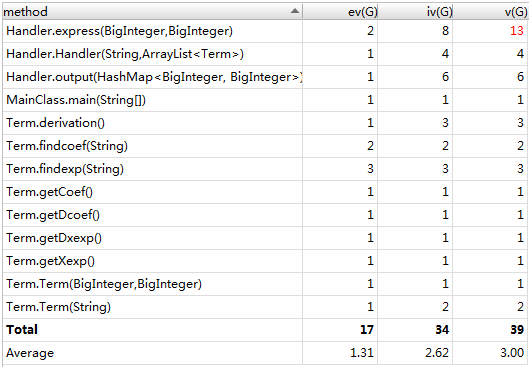
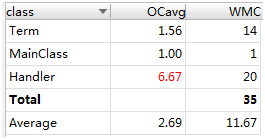
分析：Handler应当拆解为更小的模块，因为有太多的事情在Handler里面完成了，不符合高内聚低耦合原则。

第二次作业

实现方式

第二次作业在第一次作业的基础上进行迭代，更改了求导方法和输出方法，其余地方大都沿用第一次作业的代码。

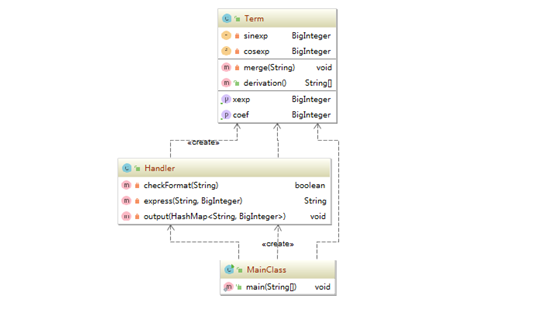
类图

代码规模

复杂度分析

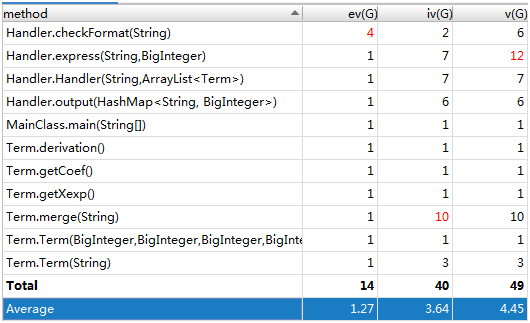
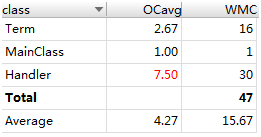
总结：可以看到checkFormat，express,merge三个方法复杂度比较高，它们共同的特点是if/else比较多，但是原因又各不相同：checkFormat是因为需要判别多种错误类型；express是因为输出的时候需要判别各种特殊情况；merge也是因为需要合并各种各样的同类项。

第三次作业

实现方式

格式判断：

1.
利用递归下降分析，在遍历字符串的同时截取各个表达式、项、因子。

2.
将各个简单因子（三角函数，幂函数）代入正则表达式看是否匹配，不匹配输出“WRONG FORMAT!”并退出程序。

预处理

1.
对于符合格式要求的输入，去除所有的空白字符。

2.
将不在括号内的部分用replace进行处理使得每一项由’+’分开。

3.
用split函数提取出项，对于每一项用’*’分开得到因子。

求导：

1.
利用递归的方式，先对于各简单因子求导，利用简单因子求导的结果得到各因子的导数，再对乘积项求导，再求出多项和的导数。

输出：

1.
利用类似递归下降分析的方式将各个项的系数和指数提取出来，将0项去除，将次幂为0、1以及系数为1、-1的项进行简化处理。

2.
将简化后的表达式输出。

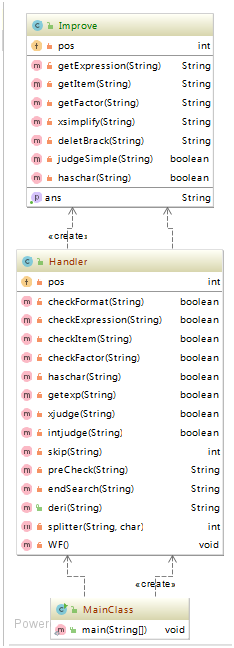
类图

代码规模

复杂度分析

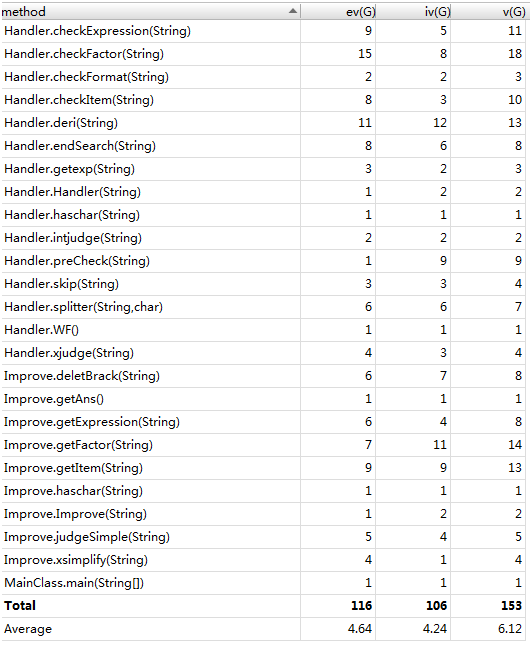
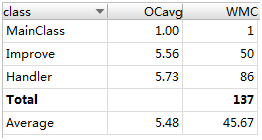
分析：本次没有红色警告，说明架构良好。

Bug分析

三次作业在中测、强测、互测中均没有发现Bug，但是我于第二次作业Hack他人3次，第三次作业Hack他人16次。发现他人Bug的主要途径有三类：

1.在自己做作业的时候曾经犯下的错误、自查到Bug的测试数据记录下来用于Hack他人。2.利用数据生成器生成一些暴力数据，对于功能进行全面检测，尝试找到他人程序中一些功能性漏洞。

3.自行编写边界数据（例如第一次作业中恰好1000个字符的边界数据，例如第二次作业中指数恰好为10000的边界数据）。

心得体会

通过这一单元的学习，我有了很大的收获。首先，我学会了利用xeger库来生产数据、用sympy来比对结果，同时还学会了使用命令行来进行输入和输出重定向；其次，我培养了自己全面思考问题的能力，正是有了在构思阶段对于可能出现情况全面的考虑，才有了这整一单元没有Bug的良好结局。

但同时，我也应当看到自己的不足。首先，我在第二次作业到第三次作业中经历了重构，但实际上第二次作业和第三次作业的要求是很相似的，只不过多了一些嵌套而已，这说明我第二次作业中采用的架构出现了问题，没有预留下可以继续迭代的空间。其次，我的程序更加面向过程而非面向对象，对于代码的封装性并不好，同时没有合理的创建对象导致在优化起来无法达到很好的效果，因为如果没有把不同的因子都存在某一个对象里而只是靠字符串的处理完成求导显然是无法化到最简的。最后，没有尝试去运用工厂模式、try/catch异常处理等方法，而只是运用了最基本的语法知识，从学习的角度上讲这是不够的。