（课内）信安数基RSA-基础&&解密加速

RSA基本实现

　　

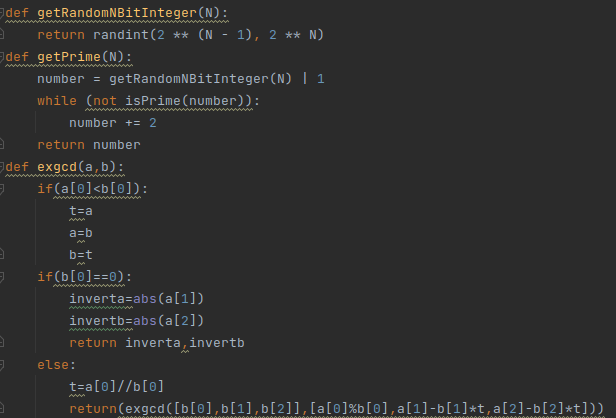
　　首先获得N比特的伪随机数；使用Random库中内容。

　　　　randint(n,m) 表示生成一个在n和m之间的随机数， **表示乘幂。

　　getPrime找素数，or 1运算是一种优化；如果当前数不是素数，则+2再验证；方法有点糙，但勉强能用。

　　exgcd此处用来计算逆元。它读取两个三元组，模仿上课时的那种矩阵解法来解。

　　　　注意else里的exgcd外一定要套return；要不然值是出不来的。

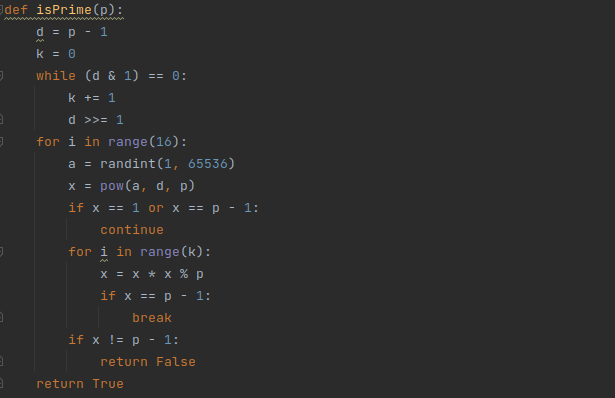
　　这里的素数判断用miller_Rabin测试写出。

先用k提取出p-1里2的所有因子，循环随机生成a，验证其是否是p的miller_Rabin witness；

pow不会出现负数，此处的p-1对应课上的-1情况；进行16次验证后未找到witness，认为其为素数。

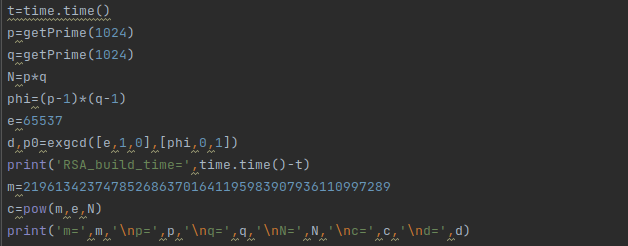
函数写好之后，就可以进行生成了。此处的代码还测试了生成所需时间；

我的测试结果基本在0.4-4s之间波动。

RSA解密加速

　　原理

　　

代码：（没啥好解释的）

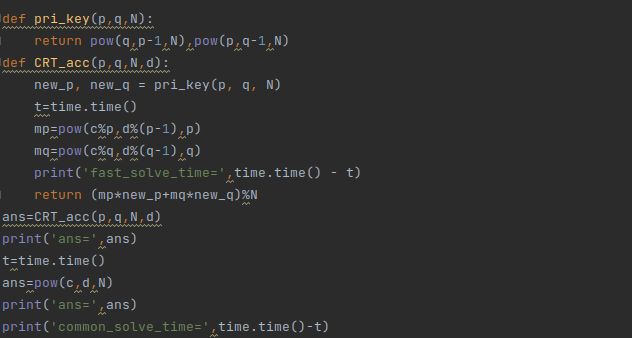
对于能够用pow实现的东西，就没有自己写平方乘之类的继续优化。

测试效果明显。