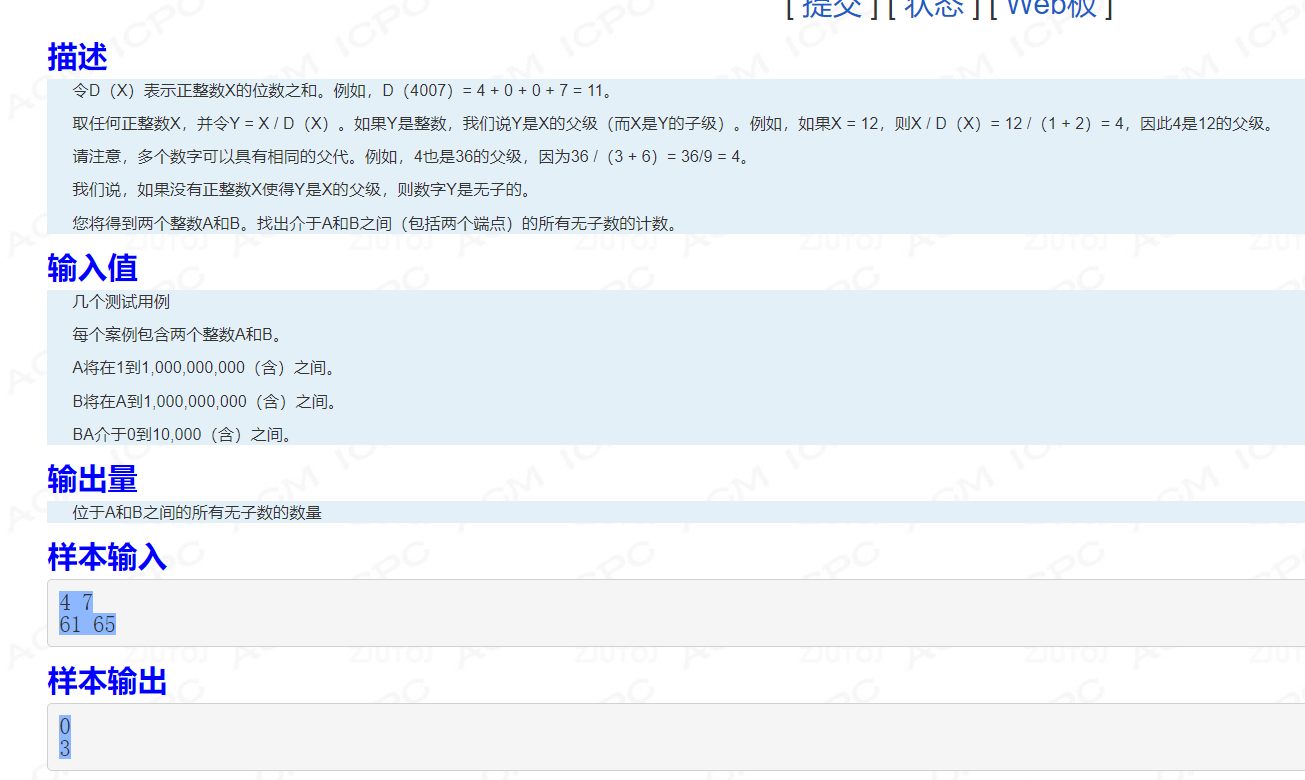
C++之无子数

题目如下：

  1 #include <iostream>
  2
  3 using namespace std;
  4
  5
  6 bool isThisNumhaveChild(int num);
  7
  8
  9 int main()
 10 {
 11     int begin_num1,end_num1,nochild_count1 = 0;
 12     int begin_num2,end_num2,nochild_count2 = 0;
 13     cin >> begin_num1 >> end_num1;
 14     cin >> begin_num2 >> end_num2;
 15     //分别调用这个函数
 16     for(int i = begin_num1; i <= end_num1;i++)
 17     {
 18         bool flag = isThisNumhaveChild(i);
 19         if(!flag)
 20         {
 21             nochild_count1++;
 22         }
 23     }
 24     for(int i = begin_num2; i <= end_num2;i++)
 25     {
 26         bool flag = isThisNumhaveChild(i);
 27         if(!flag)
 28         {
 29             nochild_count2++;
 30         }
 31     }
 32     cout << "无子数是" << nochild_count1 << "个" << endl;
 33     cout << "无子数是" << nochild_count2 << "个" << endl;
 34 /*
 35     int flag1 = isThisNumhaveChild(61);
 36     int flag2 = isThisNumhaveChild(62);
 37     int flag3 = isThisNumhaveChild(63);
 38     int flag4 = isThisNumhaveChild(64);
 39     int flag5 = isThisNumhaveChild(65);
 40     cout << flag1 << endl;
 41     cout << flag2 << endl;
 42     cout << flag3 << endl;
 43     cout << flag4 << endl;
 44     cout << flag5 << endl;
 45 */
 46 }
 47
 48
 49 bool isThisNumhaveChild(int num)
 50 {
 51     bool flag = false;
 52     //i是D（x），i*num是X
 53     int the_xnum;
 54     //接收一下是第几个数让他成为有子数
 55     int suppose_i;
 56     for(int i = 1;i < 1000;i++)
 57     {
 58         int a,b,c,d,e = 0;//个十百千万
 59         the_xnum = i*num;
 60         if(the_xnum/10000 >= 1)
 61         {//超过5位数 包括5位数
 62             e = the_xnum/10000;
 63             d = (the_xnum-e*10000)/1000;
 64             c = (the_xnum-e*10000-d*1000)/100;
 65             b = (the_xnum-e*10000-d*1000-c*100)/10;
 66             a = (the_xnum-e*10000-d*1000-c*100 -b*10);
 67             suppose_i = a + b + c + d + e;
 68         }else if(the_xnum/1000 >= 1)
 69         {//4位数
 70
 71             d = the_xnum/1000;
 72             c = (the_xnum-d*1000)/100;
 73             b = (the_xnum-d*1000-c*100)/10;
 74             a = (the_xnum-d*1000-c*100 -b*10);
 75             suppose_i = a + b + c + d;
 76         }else if(the_xnum/100 >= 1)
 77         {//3位数
 78             c = the_xnum/100;
 79             b = (the_xnum-c*100)/10;
 80             a = (the_xnum-c*100 -b*10);
 81             suppose_i = a + b + c;
 82         }else if(the_xnum/10 >= 1)
 83         {//2位数
 84             b = the_xnum/10;
 85             a = (the_xnum -b*10);
 86             suppose_i = a + b;
 87         }else
 88         {//1位数
 89             a = the_xnum;
 90             suppose_i = a;
 91         }
 92
 93         if(suppose_i == i)
 94         {
 95             //D(x) 和 应该D（X）的是一样的   break出来
 96             //flag = i;
 97             flag = true;
 98             break;
 99         }
100     }
101     return flag;
102 }

notes：

1.从line11到line33的代码冗余太多，且可修改性不高，如果要改成接收再多行的数据就捉襟见肘，待优化。

2.判断他是否有子的算法太简单了，时间复杂度大，算法待优化。

3.判断他是几位数时要注意不要忘记  =  了！！我就是这里错了结果多花了好多时间===