CUDA计算矩阵相乘

1.最简单的 kernel 函数

__global__ void MatrixMulKernel( float* Md, float* Nd, float* Pd, int Width)
{
    int tx = threadIdx.x; // cloumn
    int ty = threadIdx.y; // row

    float Pvalue = 0;

    for (int k = 0; k<Width; k++)
    {
        float Mdele = Md[ty*Width + k];
        float Ndele = Nd[k*Width + tx];
        Pvalue += Mdele * Ndele;
    }

    Pd[ty*Width + tx] = Pvalue;
}

2.适用更大矩阵

第一节中例子缺点是，假如使用更多的块时，每个块中会计算相同的矩阵。而且矩阵元素不能超过512个线程（块最大线程限制）。

改进方法是，假设每个块维度都是方阵形式，且其维度由变量 TILE_WIDTH 指定。矩阵 Pd 的每一维都划分为部分，每个部分包含 TILE_WIDTH 个元素。

#define TILE_WIDTH 4
#define Width 8

__global__ void MatrixMulKernel( float* Md, float* Nd, float* Pd, int Width)
{
    int Col = blockId.x*TILE_WIDTH + threadIdx.x; // cloumn
    int Row = blockId.y*TILE_WIDTH + threadIdx.y; // row

    float Pvalue = 0;

    for (int k = 0; k<Width; k++)
    {
        Pvalue += Md[Row*Width + k] * Nd[k*Width + Col];
    }

    Pd[ty*Width + tx] = Pvalue;
}

dim3 dimGrid(Width/TILE_WIDTH, Width/TILE_WIDTH);
dim3 dimBlock(TILE_WIDTH, TILE_WIDTH);

CUDA 硬件相关概念

针对 GT200而言

• 每个 SM 有最多8个块
• 每个 SM 有最多1024个线程

应当注意每个块中分配的线程数，以便能够充分利用SM

• 以32个线程为一个 warp，warp 为线程调度单位

3.通过改变储存器提到访问效率

CGMA（Compute to Global Memory Access），尽量提高CGMA比值。

对前面来说，每个for循环内需要两次访问全局内存（Md[Row*Width + k]， Nd[k*Width + Col]），两次浮点计算（加法与乘法）。因此 CGMA 为2:2 = 1。

G80 全局存储器带宽为 86.4 GB/s，计算峰值性能 367 Gflops。（每秒取 21.6G 个变量，由于CGMA=1，会进行 21.6G 次浮点计算）

若每个单精度浮点数为 4 字节，那么由于存储器限制，最大浮点操作不会超过 21.6 Gflops。

| 存储器类型 | 变量 | 周期 | 特点 | 访问速度 |

| --- | --- | --- | --- |

| 共享存储器 | 共享变量 | kernel函数 | 每个块中所有线程都可以访问，用于线程间协作高效方式 | 相当快，高度并行访问 |

| 常数存储器 | 常数变量 | 所有网格 | 相当快，并行访问 |

| 寄存器 | 自动变量 | 线程 | 寄存器具有储存容量限制 | 非常块

| 全局存储器 | 全局变量 | | 用于调用不同kernel函数时传递信息 | 慢 |

减少全局存储器流量策略

各个存储器特点：

• 全局存储器，容量大，访问慢
• 共享存储器，容量小，访问块

新算法要点：

• 将共享存储器上数据划分子集，每个子集满足共享存储器容量限制
• 通过线程协作将 M 和 N 中的元素加载到共享存储器中，每个线程负责块中一个元素赋值（Mds[threadIdx.y][threadIdx.x]，Nds[threadIdx.y][threadIdx.x]）
• 通过加载到共享存储器，使得每个块访问全局内存的次数减小为原来的 TILE_WIDTH 分之一（加载到共享内存时读取一次，每个块中使用 TILE_WIDTH 次）

__global__ void kernel_tile(float* M, float* N, float* P){
	int i, k;
	float Pvalue = 0;

	__shared__ float Mds[tile_width][tile_width];
	__shared__ float Nds[tile_width][tile_width];

	int Row = threadIdx.y + blockIdx.y*tile_width;
	int Col = threadIdx.x + blockIdx.x*tile_width;

	for( i = 0; i< width/tile_width; i++ ){
		Mds[threadIdx.y][threadIdx.x] = M[Row*width + i*tile_width + threadIdx.x];
		Nds[threadIdx.y][threadIdx.x] = N[(threadIdx.y + i*tile_width)*width + Col];
		__syncthreads();
		for (k = 0; k<tile_width; k++){
			Pvalue += Mds[threadIdx.y][k]*Nds[k][threadIdx.x];
		}
		__syncthreads();
	}
	P[Row*width + Col] = Pvalue;
}

存储器容量限制

G80 硬件中

• 每个 SM 寄存器大小为 8 KB（8192 B）
• 每个 SM 共享内存大小为 16 KB
• 若每个 SM 中容纳线程数为 768，那么每个线程可用寄存器不超过 8 KB/768=10 Bytes（两个单精度变量占用 8 Bytes）
• 若每个线程占用了多余 10 Bytes，那么就会减少 SM 上线程数，且以块为单位减少
• 若每个 SM 中容纳 8 个块，那么每个块不能使用超过 2 KB 的存储器

4.数据预取

在 CUDA 中，当某些线程在等待其存储器访问结果时，CUDA 线程模型可以通过允许其他 warp 继续运行，这样就能容许长时间的访问延时。

为了充分利用此特性，需要当使用当前数据元素时预取下一个数据元素，这样就可以正价在储存器访问和已访问的数据使用指令之间的独立指令的数目。

预取技术经常和分块技术结合，解决带宽限制和长时间延迟问题。

例如在第三节中矩阵乘法问题中，使用预取技术后函数流程变为

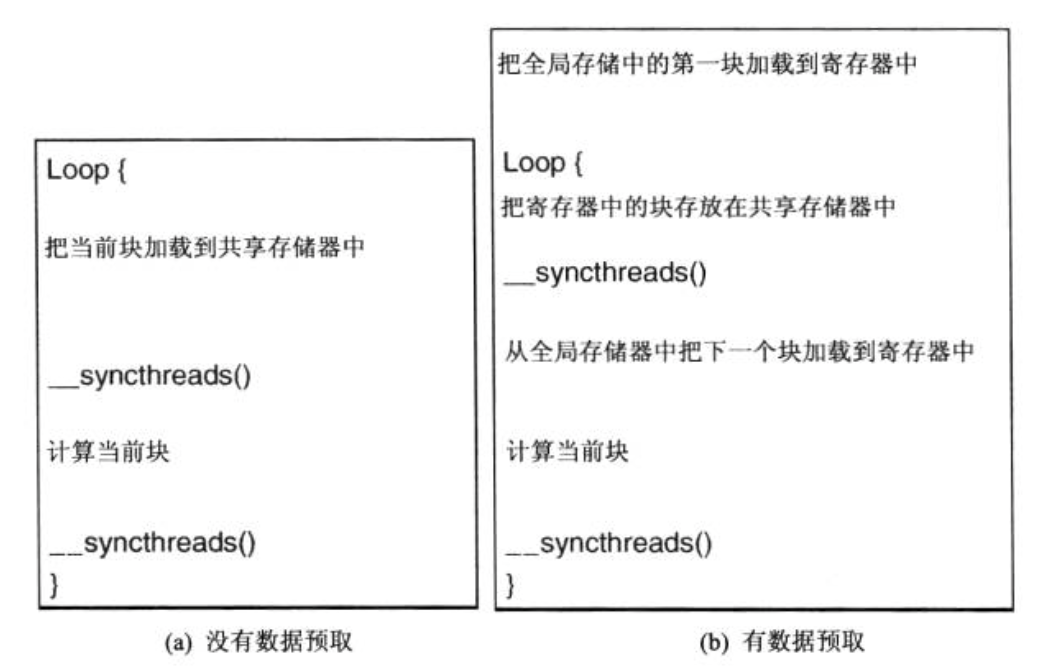
对应程序为

__global__ void kernel_prefetch(float* M, float* N, float* P){
	int i;
	float Pvalue = 0;
	float Mc, Nc;
	int Row = threadIdx.y + tile_width*blockIdx.y;
	int Col = threadIdx.x + tile_width*blockIdx.x;

	__shared__ float Mds[tile_width][tile_width];
	__shared__ float Nds[tile_width][tile_width];

	Mc = M[Row*width + threadIdx.x];
	Nc = N[Col + threadIdx.y*width];

	for (i = 1; i<width/tile_width+1; i++){

		Mds[threadIdx.y][threadIdx.x] = Mc;
		Nds[threadIdx.y][threadIdx.x] = Nc;

		__syncthreads();

		Mc = M[Row*width + threadIdx.x + i*tile_width];
		Nc = N[Col + (threadIdx.y + i*tile_width)*width];

		for (int k = 0; k<tile_width; k++){
			Pvalue += Mds[threadIdx.y][k]*Nds[k][threadIdx.x];
		}
		__syncthreads();
	}
	P[Col + Row*width] = Pvalue;
}

Mc，Nc 为增加的两个储存在寄存器内的变量。