SVD分解

首先，有y = AX，将A看作是对X的线性变换

但是，如果有AX = λX，也就是，A对X的线性变换，就是令X的长度为原来的λ倍数。

*说起线性变换，A肯定要是方阵，而且各列线性无关。（回想一下，A各列相当于各个坐标轴，X各个分量相当于各个坐标轴的“基本向量”长度）

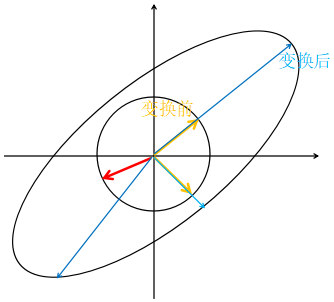（同一长度的各个方向的向量，变换前和变换后，有些前后只是拉伸了，方向不变；有些拉伸了，方向同时也改变了）

这样的X₁，X₂……X_n称为特征向量， λ₁, λ₂…… λ_n为对应的特征值。

如果有S矩阵，全是特征特征向量，也就是 S = [X₁，X₂……X_n]

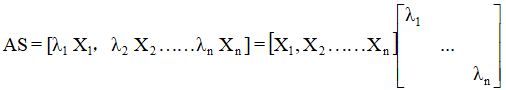
AS=S∧，A = S∧ S^-1 ，又叫矩阵对角化。（这是继LU分解，QR分解后的第三种分解）

(A = x₁λ₁ y₁  + …… + x_nλ_n y_n  ， y₁ ~ y_n 假设是S^-1 的行向量，如果λ₁ 是最大的，比其他大很多，那么对于A矩阵，只要记住x₁λ₁ y₁ 就可以有一个近似的A' ，实现了对矩阵的压缩存储)

*如果A能对角化，除了是方阵，还要各个λ值互不相同。因为λ有一对相同，证明X会有一对线性相关，从而S的列向量不独立，从而S没有逆。

---

既然这样，那么X可以单位化，也就是X' = X / ||X||，而 λ' =  ||X|| λ , X重要的是方向，而不是长度。

---

如果A是对称矩阵，那么A = A^T 

A = S∧ S^-1 = (S∧ S^-1)^T =  (S^-1) ^T ∧S^T

要式子成立，那么S^-1 = S^T ，要有这种性质的矩阵S，只有标准正交矩阵Q，因为QQ^-1 = I = QQ^T 

对于A = A^T ，有A =  Q ∧Q^T ,  并没有什么约束条件 (Gilbert Strang《Introduction to LINEAR ALGEBRA》p330)，这就是对称矩阵对角化

（对称矩阵一定是方阵，但不一定有逆，如元素全是1的也对称，但各列向量不独立）

---

 相似矩阵：如果M可逆，那么B = M^-1AM相似于A，而且B的特征值和A的特征值一样。

证明：B = M^-1AM 等价于 A = MBM^-1 , AX =λX，(MBM^-1)X=λX ,  B(M^-1X) =  λ(M^-1X)。因此，B的特征向量是(M^-1X) ，特征值依然是λ。

---

任意正交向量组V₁，V₂，V₃，通过A变换（A可以是任意形式的矩阵），得到的向量都是正交的。

（这种任意m*n的变换，应该叫“仿射变换”，因为向量v变换后，其维数都不同了；而平时n*n的变换，应该叫线性变换，维数还是一样的）

证明：A是m*n的，v是n*1的，u是m*1的，那么：

Av₁ = u₁ ，

Av₂ = u₂

要证明U₁^TU₂=0

(Av₁) ^T(Av₂ ) =u₁^Tu₂   只要证明等式左边等于0

v₁^T A^T Av₂  = u₁^Tu₂　因为A^TA是对称矩阵，所以有：

v₁^T Q ∧Q^Tv₂  = u₁^Tu₂

---

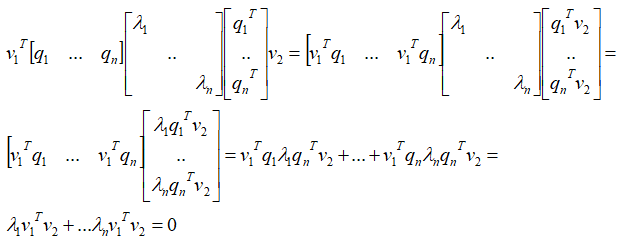
基于上面，假如将u单位化，v单位化，那么有：

Av₁ = δ₁u₁ ，

Av₂ = δ₂u₂

1. v的向量个数，顶多有n个，因为V为n维空间，n维空间中相互垂直的向量顶多有n个。

2. 就算v是长度为1，通过乘以矩阵A后，也有可能变为长度不为1的u，

假设所有n个相互正交的单位v向量，通过A变换后，得到相互正交的n个u向量， 将上式子写成矩阵形式：

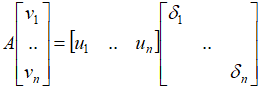
也就是：AV=UΣ

因为V是标准正交矩阵，所以VV^T=I，所以：A=UΣV^T 这就是著名的奇异值分解(SVD)

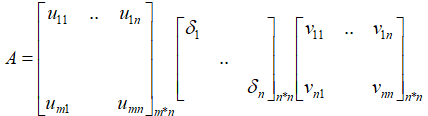
（奇异值分解，其实是通用的，终极的分解方式。一旦做SVD分解，自然会根据矩阵的特性，变为：1. 可逆且特征值不重复的方阵分解为S∧ S^-1  ；2. 对称方阵分解为Q ∧Q^T   ；3.  最一般的形式）

---

那么，现在的问题仅仅是，如何寻找V和U？

首先，我们已经知道，任意矩阵A，能分解为A=UΣV^T , 所以，可以从这个入手：

(1)AA^T =UΣV^T VΣ^T U^T

因为上式子中，V为单位正交矩阵，V^TV = I，Σ为对角矩阵，ΣΣ^T = Σ²，所以有：

AA^T = UΣ² U^T  , 这不就是对称矩阵对角化 ：U原来是AA^T  的特征向量，Σ是AA^T  的特征值开根号。

同理：

(2)A^TA  = VΣ^T U^T UΣV^T

A^TA  = VΣ ²V^T ，那么：V原来是 A^TA  的特征向量，Σ是AA^T 或 A^TA   的特征值开根号。

---

顺便有：

当m>n时：

---

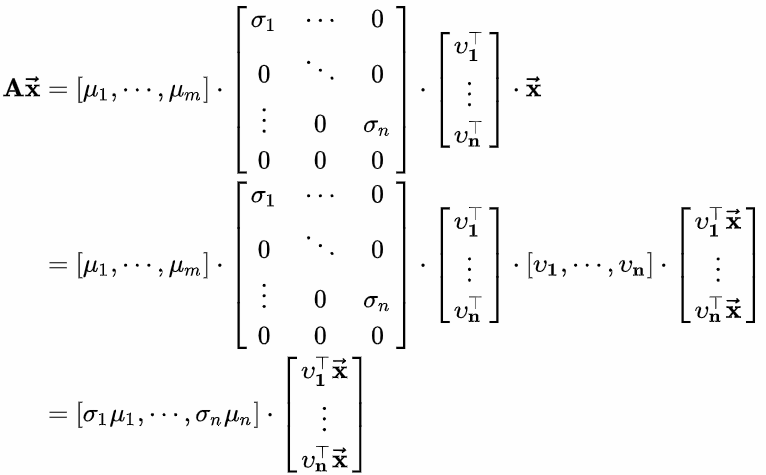
总结：计算的主要工作，是如何求解特征值的问题。这是《数值分析》的内容，在此不讲，只讲非数值分析的思路：

因为：AX =λX ，所以，(A-λI)X= 0

又因为X要有解，又不能全为0，所以A-λI 的各列要线性相关。

又因为A-λI 的各列要线性相关，所以行列式det(A-λI) = 0

(三维)行列式的几何意义是，三个向量作为边，形成的立体体积。

如果三个向量线性相关，那么自然被“压缩”到一个平面上，体积为0；

那么，只要用到 A-λI 的各列来求体积为0，就可以对λ列方程，就可以解λ。（实际上《数值分析》并不会这么解，是通过A*A*A*A....迭代得到的）

---

参考：

https://zhuanlan.zhihu.com/p/57803955 (推导过程)

https://zhuanlan.zhihu.com/p/42896542 (图片压缩和应用)