R-2 - 正态分布-中心极限-置信区间-正态假设检验

本节内容

1：样本估计总体均值跟标准差，以及标准误

2：中心极限定理

3：如何查看数据是否是正态分布QQ图

4：置信区间的理解跟案例

5：假设检验

参考文章：

假设检验的学习和理解

一、样本估计总体均值跟标准差

多组抽样

    估计总体均值 = mean（多组的各个均值）

    估计总体标准差 = sd(多组的各个标准差)

    标准误 =  sd（多组的各个均值）

一组抽样

    估计总体均值 = mean（一组的均值）

    估计总体标准差 = sd(一组的标准差)

    标准误 =  估计的标准差/ sqrt(n)

标准误：

    真实的标准误 = 总体方差 / sqrt(n)  ##n个样本的真实标准误

    标准误==是描述样本均值的稳定性	

标准误很重要：

　　比如说让你去估计全校的平均身高，

　　你给如个一个1.7，还要给出一个置信区间，可行程度有多少？
　　怎么给呢？这就需要用到标准误了

　　置信区间就是，样本均值跟标准误计算出来的。

代码实现样本估计总体

set.seed(1)

xset =rnorm(300,1.7,2.4)

##多组抽样估计总体均值和方差

ms = matrix(sample(xset,20*20,replace = T),20,20)  ##一行就是一组抽样数据

me5 = mean(rowMeans(ms))

sde5 = numeric()

for (i in 1:20){

  sde5[i] = sd(ms[i,])

  print(sd(ms[i,]))

}

sde5 = mean(sde5)

print(me5)  ## 1.749969

print(sde5) ##2.360055

##只抽取一组估计均值和方差

data1 = sample(ms,20)

mean(data1)  ##1.418414

sd(data1)   ##2.43754

##标准误--》说的是均值的标准误

#一组的标准误

(sd(data1))/sqrt(20) #0.5073691

#多组的标准误

sd(rowMeans(ms))  ##0.4417979

#一组数据真实的标准误

2.4/sqrt(29)  ##0.4456688

二、中心极限定理

当样本量足够大的时候，样本的均值就服从正态分布！！！

当样本比较小的时候才会存在别的分布如t分布。

为什么要对数据进行取log

当你的数据分布是严重右偏的函数，我们要对数据取log，将数据分布变成偏向正态的分布。

为什么要这么做，就是为了让它更加的去适用于中心极限定理。

三：如何查看数据是否是正态分布QQ图

q = rnorm(4000)

s3 = sample(q,300)

qqnorm(s3)

qqline(s3)   ##点离线越接近，越正态

四、置信区间的理解跟案例　

4.1：置信区间是什么意思：

比如说置信区间或者可信程度为95%，就是说100次的抽样，有95次在总体均值范围。

4.2：置信区间计算公式：

4.3：数据服从正态分布时统计量的计算

#当可信程度为95%的时候的统计量,我们说的95%是区间中间的百分95

qnorm(1-(1-0.95)/2))

#(1-0.95)/2 
#求的是中间围绕95%的时候的累计概率是多少 
#qnorm(累积概率) 得出对应的x轴数值 --》统计量

4.4：1-（1-pnorm(3))*2 怎么理解？

#三倍标准差所围绕中间的面积

#pnorm(3)求出来的是三倍标准差的累计概率是多少

#1-pnorm(3) 就求出了剩下的概率

#1-（1-pnorm(3))*2  1-剩下概率*2  就是三倍标准差所围绕中间的面积

4.5：案例

读取一份数据，是房价的增长率，作为增长率的95%的置信区间

head   tail  读取文件的前【后】几行

hist(rate,freq=F) ##将直方图的y轴频数变成密度

lines（desity(rate)） ##做出密度曲线

mean(rate)+c(-1,1)*qnorm(1-(1-0.95)/2)*sd(rate)/sqrt(150)

##抽样的均值 加减  统计量*(标准误）

五、假设检验

5.1：假设检验，形式化的可以总结为以下6步：

确定原假设H₀和备选假设H₁
根据H₀，确定统计量的概率分布和相关参数
确定显著性水平α和拒绝域
根据步骤2的参数，求出P值
查看P值是否位于拒绝域以内
做出判断，如果P值在拒绝域以内，那么拒绝H₀接受H₁。否则接受H₀拒绝H₁

5.2：假设检验出现的两种错误：

上面提到，假设检验不会100%确保检验结果正确，会出现上面的两类错误：

第一类错误：错误的拒绝原假设。原假设正确，但是却错误的拒绝了，发生此事件的概率为α，也就是显著性水平。所以显著性水平越高，越容易发生。
第二类错误：错误的接受原假设。原假设错误，但是却接受了原假设。发生此事件的概率需要根据统计量的分布，和被选项假设具有具体值来确定，这里先略过（《Head First Statistics》假设检验这一章中举了一个例子描述如何求解其概率）。

5.3：关于如何选取显著性水平：

显著性水平α一般为0.05，但是根据需要可以设为0.1或者0.01。当α较大时，第一类错误的概率增大，第二类错误的概率减少；α较小时，则相反。下面举几个例子：

例1 一个汽车制造商正在考核新零件，该零件对车辆安全至关重要。目前正在抽样检测，你觉得α应该如何指定。

解答H₀：新配件与原始配件的安全性能相同。H₁：新配件比原始配件更安全。由于此配件关系用户声明安全，所以需要尽量使用较安全的配件，拒绝假设H₀，那么可以设将α设置高一点，比如 0.1。

例2 一个机器中，有一个配件，替换成本十分高，但是如果该配件损坏了，对机器影响不大，请问显著性水平应该如何选取。

解答 H₀：配件正常工作。H₁：配件损坏。由于替换成本较高，所以需要确保零配件的确损坏才能替换，可以将α设置较小，比如0.01。

5.4：如何理解假设检验的两种错误

我们取了栗子：

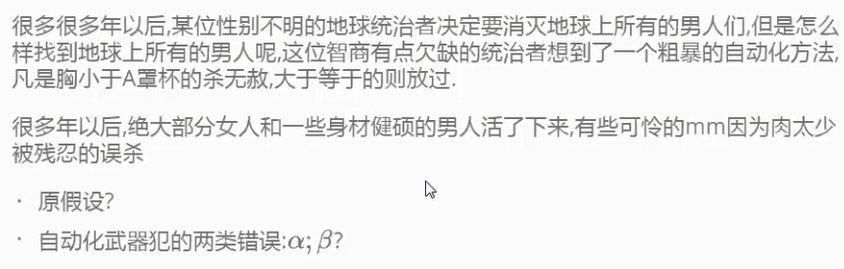
问题1：原假设是什么？

原假设H0：这个人是女

备假设H1: 这个人是男

问题2：女士误杀为第一类错误，男士存活为第二类错误如何画图？

图中：

1：H0为女的分布，H1为男的分布。X轴是罩杯，我们判断大于等于B的是女，然后画红线。

2：H0的分布在红线右边是误杀的，H1的分布在红线左边是存活的。

3：我们就可以时理解说：女士误杀的为检验的第一类错误，男士存活为检验的第二类错误。

4：将男士存活的记作β（贝塔），女士误杀的为α（阿尔法），正确杀了男士的为统计功效=1-β

5：在统计学上：一般将α标记为0.05 β可容忍程度为20%，也就是1-β找出正确的概率为80%。

6：α和β，可以从图中看出，二者是有相关的，当α取的小就形成了---宁错杀不放过的寓意。

统计功效

是正确找出的概率

常常在医学等研究不仅仅给出p值就可以了，还需要给出统计功效。

问题3：对统计功效的延伸--》

很多时候我们不是说只是根据显著性就可以判断事件的，还要判断基数谬误的，特别是在医学上的一些问题。

如：我们有100种药物，有效的为5种，无效的为95种，利用统计学判断正确找出药物的概率

H0：这个药物无效

H1：这个药物有效

显著性取==0.05 --》那么也就是说我们允许有0.05的误差，会将无效药物看成有效药物有 95*0.05≈5种

统计功效==1-β=80%--》那么从正确的药物找出是有效的有 5*0.8 = 4种

也就是说我们一共找出了9种药物是有效的，可是实际仅仅只有5种，

那么我们这次的概率为5/9 = 44%的可信度，找出的9种药物它的可信程度只有44%

5.5：假设检验案例