洛谷 P4710 「物理」平抛运动

题目描述

小 F 回到班上，面对自己 28 / 110 的物理，感觉非常凉凉。他准备从最基础的力学学起。

如图，一个可以视为质点的小球在点 A(x_0, y_0)A(x0,y0) 沿 xx 轴负方向以某速度抛出，无视除重力外的所有阻力，最后恰好以速度 vv 砸到 B(0, 0)B(0,0) 点。

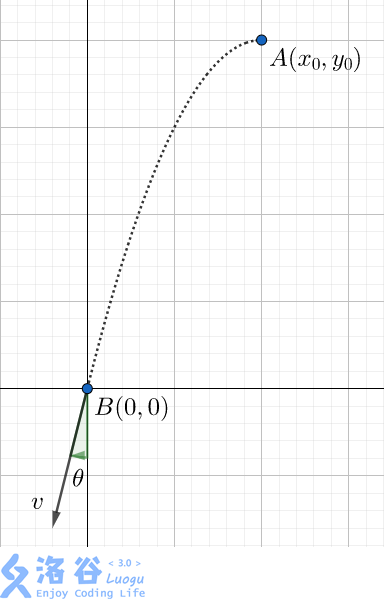
给定 vv 的大小与方向，你的任务是求出 (x_0,y_0)(x0,y0)。

给定的速度单位为 m \cdot s ^ {-1}m⋅s−1，重力加速度 g = 10 \ (m \cdot s ^ {-2})g=10 (m⋅s−2)，请输出以 mm 为单位的答案。

如果你没有学过相关内容也没有关系，你可以从样例和提示里理解该题所求内容。

输入格式

输入一行，为两个最多 66 位的小数 v, \theta(1 \leq v \leq 100, 15 ^ \circ \leq \theta \leq 75 ^ \circ )v,θ(1≤v≤100,15∘≤θ≤75∘)，即速度与图中所标角在弧度制下的大小。

输出格式

输出一行，两个最多 1515 位的小数 x_0, y_0x0,y0，为你的答案。

你的答案与参考答案的相对误差或者绝对误差小于 10 ^ {-3}10−3 即视为正确。

输入输出样例

输入 #1复制

输出 #1复制

说明/提示

样例解释

如图。

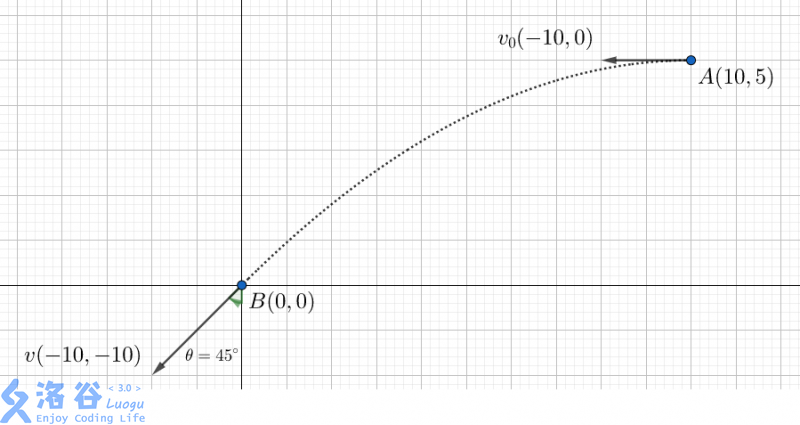
14.142136 \approx 10 \sqrt 2, 0.785398 \approx \frac \pi 4 = 45 ^ \circ .14.142136≈102,0.785398≈4π=45∘.

小球从 (10, 5)(10,5) 以速度 (-10, 0)(−10,0) 抛出，即可在 t = 1st=1s 时以 (-10, -10)(−10,−10) 砸在 (0, 0)(0,0)。

提示

如果你没有学习过相关内容，下面的内容可能有帮助：

zcy 教你学物理

首先，由于单位均为标准单位，所以所有结果均可以直接数字运算；视为质点意味着没有体积。

我们可以将小球速度分解，如图：

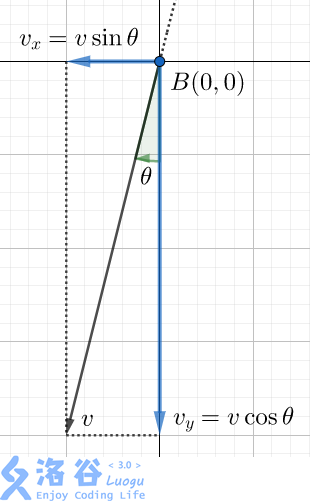
其中水平方向上的速度 v_xv**x 即为抛出速度，运动过程中一直为 v \sin \thetavsinθ；

垂直方向上的速度 v_yv**y 受重力加速，由 00 变化至 v \cos \thetavcosθ。

从抛出时开始计时，当时间为 tt 时，设此时水平、垂直方向上速度的大小分别为 v_{xt}, v_{yt}vxt,vyt，水平、垂直方向上位移的大小分别为 x_{xt}, x_{yt}xxt,xyt，有：

v_{xt} = v \sin \thetavxt=vsinθ

v_{yt} = gtvyt=g**t

x_{xt} = v_{xt}txxt=vxt**t

x_{yt} = \frac 1 2 g t ^ 2 = \frac 1 2{v_{yt}t}xyt=21g**t2=21vyt**t

当 tt 恰好是落地时间时，x_{xt}, x_{yt}xxt,xyt 即为答案。

关于弧度制：

\pi = 180 ^{\circ}π=180∘

也就是说：\frac \pi 2 = 90 ^{\circ}, \frac \pi 3 = 60 ^{\circ}, \ \cdots2π=90∘,3π=60∘, ⋯

关于三角函数：

如果你是 C/C++ 选手，你可以使用 math.h / cmath 里的 sin() cos() 进行计算；

如果你是 Pascal 选手，你可以使用 math 库（在 begin 前添加 uses math;）里的 sin() cos() 进行计算。

如果你是 Python 选手，你可以使用 math 库里的 math.sin() math.cos() 进行计算。

如果你是其他语言的选手，请参考相应文档。

题解：

这题真的是一道物理题...高一文化课蒟蒻表示不太会做...

但这题其实准备知识都告诉你了：平抛运动可以分解成一个自由落体运动和匀速直线运动。矢量运算用平行四边形法则正交分解法。那么我们就得到：

水平方向上的速度\(v_x\)为抛出的速度，运动过程中为\(v\times sin(\alpha)\)（原谅我不会打cita）。而垂直方向上的速度还要加一个加速度\(g=10m/s^2\).那么就是从\(0\rightarrow v\times cos(\alpha)\)。很容易得出，这个东西还跟时间有关系。

从抛出的时候开始计时：当时间为\(t\)时，设此时的水平、竖直方向上的速度大小分别为：\(v_x,v_y\).

那么有：

\[v_x=v\times sin(\alpha)
\]

\[v_y=v\times cos(\alpha)
\]

\[v_y=gt
\]

所以，可以通过上面的那些式子搞吧搞吧得到一个运动时间的式子：

\[t=\frac{v_y}{g}
\]

因为在水平方向质点相当于做匀速直线运动，所以水平方向上的位移\(x_0\)可以被表示为：

\[x_0=v_x\times t
\]

根据三角形相似，对应边成比例，所以有：

\[(\frac{x_0}{2}):y_0=v_x:v_y
\]

变形：

\[y_0=\frac{x_0}{2}\times \frac{v_y}{v_x}
\]

所有的式子都在上面了，通过已知量可以解出两个未知量：\(x_0,y_0\)。

代码如下：

#include<cmath>

#include<cstdio>

double v,cita,vx,vy,t,x2;

const double g=10.0;

int main()

{

    scanf("%lf%lf",&v,&cita);

    vy=v*cos(cita);

    vx=v*sin(cita);

    t=vy/g;

    x2=v*sin(cita)*t;

    printf("%.3lf %.3lf\n",x2,(x2/2)*vy/vx);

    return 0;

}