F-maximum clique 1_2019牛客暑期多校训练营（第五场）

题意

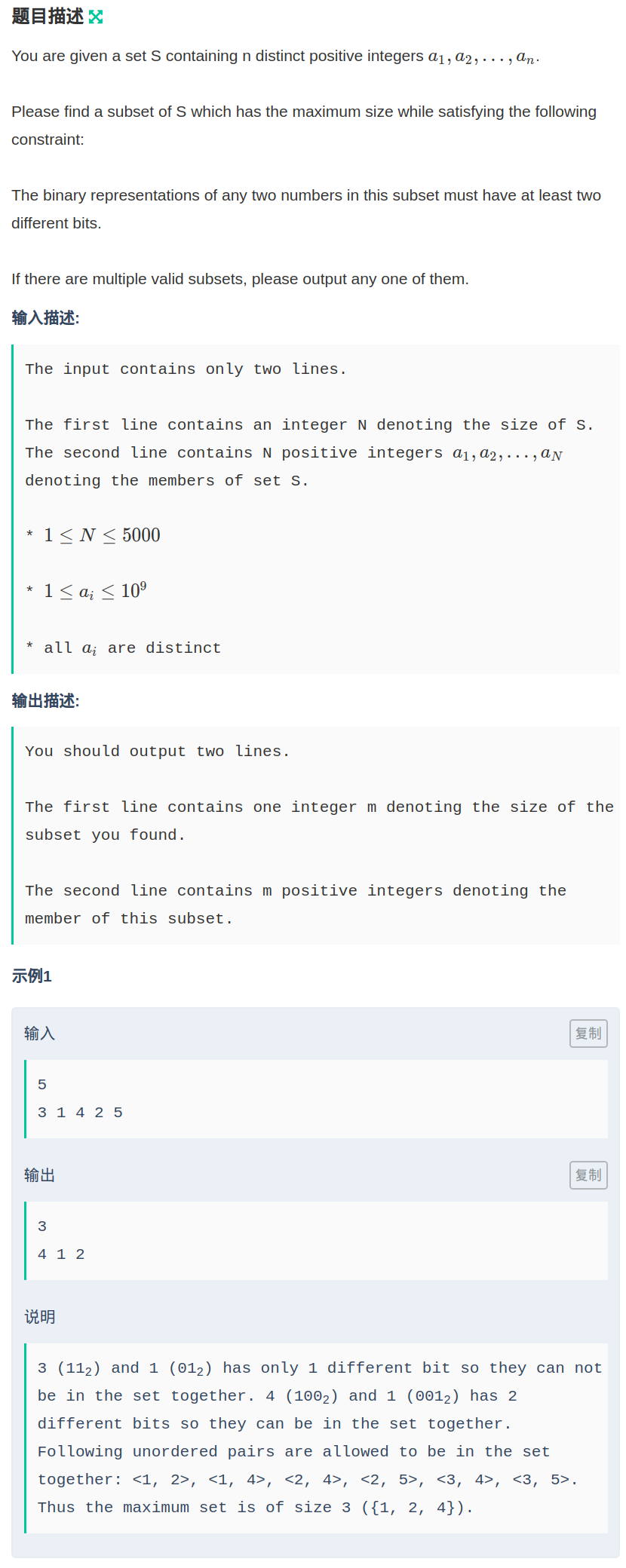
给出n个不同的数字\(a_i\)，求出最大的子集，使得子集内任意两个数在二进制下至少有两位不同。

题解

先对任意两个二进制位只有一个不同的两个数连边，那么问题就转化成找出最多的点集，任意两点没有边，也就是最大独立集问题。普通的图求最大独立集是N-P困难的，但是二分图求最大独立集合是多项式复杂度的。

所以我们把图转换成二分图形式，把二进制下有奇数个1的数放在左边，有偶数个1的数放在右边，这样左边内的点和右边内的点一定不会有连边，因为两边的点二进制1的个数奇偶性是一样的，且不存在相同的数，那么同一边内的两个数就至少会有两位不同。

接下来就是求二分图的最大独立集，参考博客：二分图的最小顶点覆盖 最大独立集 最大团

简单说就是先用匈牙利求出最大匹配，得到包含在最大匹配内的边，对二分图右边每一个不是最大匹配边的端点的点进行一次dfs，dfs路线是未匹配边->匹配边->未匹配边这样交替，对dfs经过的所有点标记vis。最后二分图左边未标记vis，右边标记了vis的点，就是这张二分图的最大独立集

代码

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
const int mx = 5005;
const int INF = 0x3f3f3f3f;

vector <int> mp[mx];
vector <int> L, R, ans;
int a[mx], linker[mx];
bool used[mx], vis[mx];
int n;

bool dfs(int u) {
    for (int i = 0; i < mp[u].size(); i++) {
        int v = mp[u][i];
        if (!used[v]) {
            used[v] = true;
            if (linker[v] == -1 || dfs(linker[v])) {
                linker[v] = u;
                return true;
            }
        }
    }
    return false;
}

int hungary() {
    int res = 0;
    memset(linker, -1, sizeof(linker));
    for (int u = 0; u < L.size(); u++) {
        memset(used, false, sizeof(used));
        if (dfs(L[u])) res++;
    }
    return res;
}

void dfs2(int u, int flag) {
    vis[u] = true;
    for (int i = 0; i < mp[u].size(); i++) {
        int v = mp[u][i];
        if (vis[v]) continue;
        if (flag) {
            if (linker[u] != v) dfs2(v, flag^1);
        } else {
            if (linker[v] == u) dfs2(v, flag^1);
        }
    }
}

int main() {
    memset(vis, false, sizeof(vis));
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        if (__builtin_popcount(a[i]) % 2 == 1) L.push_back(i);
        else R.push_back(i);
    }

    for (int i = 0; i < L.size(); i++) {
        for (int j = 0; j < R.size(); j++) {
            if (__builtin_popcount(a[L[i]]^a[R[j]]) == 1) mp[L[i]].push_back(R[j]), mp[R[j]].push_back(L[i]);
        }
    }
    printf("%d\n", n - hungary());
    for (int i = 0; i < R.size(); i++) {
        int v = R[i];
        //printf("linker[%d] = %d\n", v, linker[v]);
        if (linker[v] == -1) dfs2(v, 1);
    }
    for (int i = 0; i < L.size(); i++)
        if (!vis[L[i]]) ans.push_back(L[i]);
    for (int i = 0; i < R.size(); i++)
        if (vis[R[i]]) ans.push_back(R[i]);

    for (int i = 0; i < ans.size(); i++) printf("%d%c", a[ans[i]], i==ans.size()-1?'\n':' ');
    return 0;
}