洛谷P2704 [NOI2001]炮兵阵地题解

题目描述

司令部的将军们打算在\(N * M\)的网格地图上部署他们的炮兵部队。一个\(N * M\)的地图由N行M列组成，地图的每一格可能是山地（用\(“H”\) 表示），也可能是平原（用\(“P”\)表示），如下图。在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：



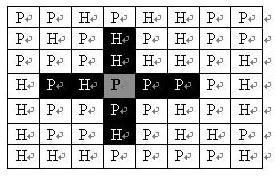
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

输入格式

第一行包含两个由空格分割开的正整数，分别表示\(N\)和\(M\)；

接下来的\(N\)行，每一行含有连续的\(M\)个字符（\(‘P’\)或者\(‘H’\)），中间没有空格。按顺序表示地图中每一行的数据。\(N≤100；M≤10\)。

输出格式

仅一行，包含一个整数\(K\)，表示最多能摆放的炮兵部队的数量。

输入输出样例

输入 #1

5 4

PHPP

PPHH

PPPP

PHPP

PHHP

输出 #1

6

解析：

\(状压DP\)

\(dfs\)求出状态和状态数

设\(N[i][j]\)表示第i行第j个状态所用的炮兵数量

设一个转移状态\(dp[i][j][k]\)是当前的炮兵数

\(i\)表示第\(i\)行，\(j\)表示第\(i\)行第\(j\)个状态，\(k\)表示第\(i-1\)行第\(k\)个状态

方程也特别简单

\(dp[i][j][k] = max(dp[i][j][k], dp[i-1][k][l] + N[i][j]);\)

然后枚举出第\(n\)行的所有状态和第\(n-1\)行的所有状态，取一个\(max\)

但是会遇到一个问题，就是数组会开的很大，这时通过\(dfs\)发现

当全都是\(P\)时，也只有\(60\)种状态，所以可以减小数组.

#include <cstdio>
#include <cstring>
#define re register
inline int read() {
	int s = 0, f = ' '; char ch = getchar();
	while(ch < '0' || ch > '9') { if(ch == '-') f = '-'; ch = getchar();}
	while(ch >= '0' && ch <= '9') s = (s << 3) + (s << 1) + ch - '0', ch = getchar();
	return f == '-' ? -s : s;
}
inline int max(int a, int b) { return a > b ? a : b;}
const int Max = 12;
const int MAX = 102;
const int INF = 0x7fffffff;
int n, m, dp[MAX][65][65];
int st[MAX][65], sum[MAX], N[MAX][65];
char ch[MAX][Max];
void dfs(int x, int Sum, int j, int p) {
	if(j > m) {
		st[x][++sum[x]] = Sum; N[x][sum[x]] = p;
		return ;
	}
	dfs(x, Sum, j + 1, p);
	if(ch[x][j] == 'P') dfs(x, Sum + (1 << j), j + 3, p + 1);
}
int main() {
	n = read(); m = read();
	for(re int i = 1; i <= n; ++ i)
		scanf("%s", ch[i] + 1);
	for(re int i = 1; i <= n; ++ i) dfs(i,0,0,0);
	for(re int i = 1; i <= n; ++ i)
		for(re int j = 1; j <= sum[i]; ++ j)
			dp[i][j][0] = N[i][j];
	for(re int i = 1; i <= sum[2]; ++ i)
		for(re int j = 1; j <= sum[1]; ++ j) {
			if(st[2][i] & st[1][j]) continue;
			dp[2][i][j] = max(dp[2][i][j], dp[1][j][0] + N[2][i]);
		}
	for(re int i = 3; i <= n; ++ i)
		for(re int j = 1; j <= sum[i]; ++ j)
			for(re int k = 1; k <= sum[i-1]; ++ k)
				for(re int l = 1; l <= sum[i-2]; ++ l) {
					if(st[i][j] & st[i-1][k]) continue;
					if(st[i][j] & st[i-2][l]) continue;
					if(st[i-1][k] & st[i-2][l]) continue;
					dp[i][j][k] = max(dp[i][j][k], dp[i-1][k][l] + N[i][j]);
				}
	int ans = -INF;
	for(re int i = 1; i <= sum[n]; ++ i)
		for(re int j = 1; j <= sum[n-1]; ++ j)
			ans = max(ans, dp[n][i][j]);
	printf("%d",ans);
	return 0;
}