文艺平衡树-splay的区间操作

　　真的是个神题，蒟蒻表示无力吐槽。刚开始以为是一个板子题，看着题解打了一遍，大概也理解了他是怎么实现的，然后我就去做别的题了，然后就在Three_D大佬的询问下蒙*了。最后还是问的nc哥，并思考了一个中午才搞明白。最主要的一点是，旋转不会改变树的中序遍历。

【建树操作】

　　对于一棵BST，区间[l,r]，如果把l-1 splay到根，把r+1 splay到根的右子树，那么[l,r]即为根的右子树的左子树，如果不是BST，这个性质同样适用。然后因为旋转可能会涉及到1，n，所以要建立1，n+2两个哨兵节点；因为平衡树维护的是一个序列，所以一开始树的中序遍历应该是原序列：

 rt=build_tree(,,n+);
 int build_tree(int fa,int l,int r)
 {
     if(l>r) return ;
     int mid=(l+r)>>,
         now=++sz;
     key[now]=data[mid];f[now]=fa;tag[now]=;
     ch[now][]=build_tree(now,l,mid-);
     ch[now][]=build_tree(now,mid+,r);
     pushup(now);
     return now;
 }

【splay】

　　rotate不改变树的中序遍历，原rotate函数不变。因为要将r+2 splay到根的右节点而不是根，所以要多传一个参：

 void splay(int x,int goal)
 {
     for(int fa;(fa=f[x])!=goal;rotate(x))
         if(f[fa]!=goal)
             rotate(get(fa)==get(x)?fa:x);
     if(!goal)rt=x;
 }

【翻转区间】*

　　对于区间[l,r],将l splay到根，r+2 splay到根的右儿子，那么r+2的左子树就是[l+1,r+1].如果将r+2的左儿子的左右子树翻转，并递归地翻转下去，那么[l+1，r+1]的中序遍历就会翻转。但是这样的时间复杂度太高，所以延续线段树中懒标记的操作。

 void turn(int l,int r)
 {
     l=rnk(l);
     r=rnk(r+);
     splay(l,);
     splay(r,l);
     pushdown(rt);
     tag[ch[ch[rt][]][]]^=;
 }

　　然后说说把我弄懵逼的东西，对于序列 [12345],平衡树如图：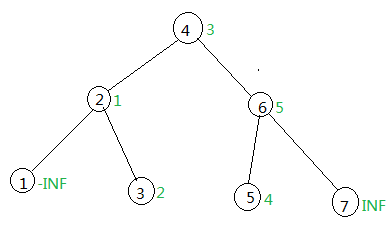

　　绿色的数字为key值，一定要注意区分节点的排名和这个节点的值，在建树时，key[now]=data[mid];当前节点的key存储的是序列的值，而图中黑色的数字是节点的排名，可能有点难以理解，那举个例子：

　　对于[12345],如果要翻转区间[2,3]，那么在平衡树中找到排名为2的数（l=rnk(l)），即2，将他旋转到根，找到排名为5的数（r=rnk(r+2)），即5，将他旋转到根的右儿子，则5的左子树为[34],key值就是所要翻转的区间[23]，打上标记，翻转完成。

Ps.除区间翻转外，还可以进行区间删除，区间加上x等操作。

【标记下传】

　　每到一个节点就要下传懒标记：

 void pushdown(int x)
 {
     if(x && tag[x])
     {
         tag[ch[x][]]=tag[ch[x][]]^;
         tag[ch[x][]]=tag[ch[x][]]^;
         swap(ch[x][],ch[x][]);
         tag[x]=;
     }
 }

【输出结果】

　　中序遍历整棵树即可：

 void write(int now)
 {
     pushdown(now);
     if(ch[now][])write(ch[now][]);
     if(key[now]!=INF && key[now]!=-INF)cout<<key[now]<<" ";
     if(ch[now][]) write(ch[now][]);
 }

【完整代码】

 #include<iostream>
 #include<cstdio>
 #include<cmath>
 #define INF 0x7fffffff
 using namespace std;
 int n,m,data[];
 int ch[][],size[],cnt[],f[],key[],tag[],sz,rt;

 int get(int x){return ch[f[x]][]==x;}
 void pushup(int x)
 {
     size[x]=size[ch[x][]]+size[ch[x][]]+;
 }
 void pushdown(int x)
 {
     if(x && tag[x])
     {
         tag[ch[x][]]=tag[ch[x][]]^;
         tag[ch[x][]]=tag[ch[x][]]^;
         swap(ch[x][],ch[x][]);
         tag[x]=;
     }
 }
 int build_tree(int fa,int l,int r)
 {
     if(l>r) return ;
     int mid=(l+r)>>,
         now=++sz;
     key[now]=data[mid];f[now]=fa;tag[now]=;
     ch[now][]=build_tree(now,l,mid-);
     ch[now][]=build_tree(now,mid+,r);
     pushup(now);
     return now;
 }
 void rotate(int x)
 {
     int old=f[x],oldf=f[old],which=get(x);
     pushdown(oldf),pushdown(old),pushdown(x);
     ch[old][which]=ch[x][which^];f[ch[old][which]]=old;
     ch[x][which^]=old;f[old]=x;
     f[x]=oldf;
     if(oldf) ch[oldf][ch[oldf][]==old]=x;
     pushup(old),pushup(x);
 }
 void splay(int x,int goal)
 {
     for(int fa;(fa=f[x])!=goal;rotate(x))
         if(f[fa]!=goal)
             rotate(get(fa)==get(x)?fa:x);
     if(!goal)rt=x;
 }
 int rnk(int x)
 {
     int now=rt;
     while()
     {
         pushdown(now);
         if(x<=size[ch[now][]])now=ch[now][];
         else
         {
             x-=size[ch[now][]]+;
             if(!x)return now;
             now=ch[now][];
         }
     }
 }
 void turn(int l,int r)
 {
     l=rnk(l);
     r=rnk(r+);
     splay(l,);
     splay(r,l);
     pushdown(rt);
     tag[ch[ch[rt][]][]]^=;
 }
 void write(int now)
 {
     pushdown(now);
     if(ch[now][])write(ch[now][]);
     if(key[now]!=INF && key[now]!=-INF)cout<<key[now]<<" ";
     if(ch[now][]) write(ch[now][]);
 }
 signed main()
 {
     cin>>n>>m;
     for(int i=;i<=n;i++)data[i+]=i;
     data[]=-INF,data[n+]=INF;
     rt=build_tree(,,n+);
     int x,y;
     for(int i=;i<=m;i++)
     {
         cin>>x>>y;
         turn(x,y);
     }
     write(rt);
     return ;
 }