luogu P1351 联合权值

题目描述

无向连通图G 有n 个点，n - 1 条边。点从1 到n 依次编号，编号为 i 的点的权值为W i ，每条边的长度均为1 。图上两点( u , v ) 的距离定义为u 点到v 点的最短距离。对于图G 上的点对( u, v) ，若它们的距离为2 ，则它们之间会产生Wu×Wv 的联合权值。

请问图G 上所有可产生联合权值的有序点对中，联合权值最大的是多少？所有联合权值之和是多少？

输入输出格式

输入格式：

输入文件名为link .in。

第一行包含1 个整数n 。

接下来n - 1 行，每行包含 2 个用空格隔开的正整数u 、v ，表示编号为 u 和编号为v 的点之间有边相连。

最后1 行，包含 n 个正整数，每两个正整数之间用一个空格隔开，其中第 i 个整数表示图G 上编号为i 的点的权值为W i 。

输出格式：

输出文件名为link .out 。

输出共1 行，包含2 个整数，之间用一个空格隔开，依次为图G 上联合权值的最大值

和所有联合权值之和。由于所有联合权值之和可能很大，输出它时要对10007 取余。

输入输出样例

输入样例#1： 复制

5
1 2
2 3
3 4
4 5
1 5 2 3 10 

输出样例#1： 复制

20 74

说明

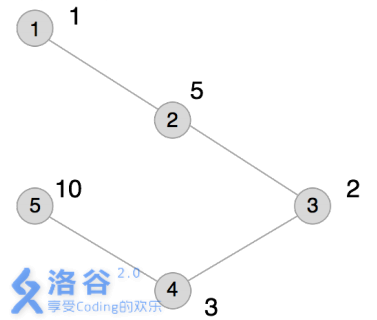
本例输入的图如上所示，距离为2 的有序点对有( 1,3) 、( 2,4) 、( 3,1) 、( 3,5) 、( 4,2) 、( 5,3) 。

其联合权值分别为2 、15、2 、20、15、20。其中最大的是20，总和为74。

【数据说明】

对于30% 的数据，1 < n≤ 100 ；

对于60% 的数据，1 < n≤ 2000；

对于100%的数据，1 < n≤ 200 , 000 ，0 < wi≤ 10, 000 。

dfs模拟权值只在祖孙，兄弟之间产生

#include<cmath>
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn =  ;
const int mod = ;
int n,a[maxn],head[maxn],num;
struct node{
    int v,next;
}edge[maxn*];
void add_edge(int a,int b) {
    edge[++num].v=b;edge[num].next=head[a];head[a]=num;
}
int max_ans,ans;
void dfs(int x,int fa,int gfa) {
    int sum=,div=,fv=,sv=;
    for(int i=head[x];i;i=edge[i].next) {
        int v=edge[i].v;
        if(v!=fa) {
            sum=(sum+a[v])%mod;div=(div+a[v]*a[v]%mod)%mod;
            if(a[v]>fv)sv=fv,fv=a[v];
            else if(a[v]>sv)sv=a[v];
            dfs(v,x,fa);
        }
    }
    ans=(ans+(sum*sum%mod-div+mod)%mod+*a[x]*a[gfa]%mod)%mod;
    max_ans=max(max_ans,max(fv*sv,a[x]*a[gfa]));
    return;
}
int main() {
    scanf("%d",&n);
    for(int aa,b,i=;i<n;++i) {
        scanf("%d%d",&aa,&b);add_edge(aa,b),add_edge(b,aa);
    }
    for(int i=;i<=n;i++) scanf("%d",a+i);
    dfs(,,);
    printf("%d %d\n",max_ans,ans);
    return ;
}