Codeforces Round #505 (rated, Div. 1 + Div. 2, based on VK Cup 2018 Final) 题解

真心简单的一场比赛 就是坑比较多（自己太蠢）

A是一个水题 3分钟的时候过了

B也是一个比较简单的题 类似的套路见得多了 但是我当时可能比较困 想了一会才想出来 19分钟的时候过掉了

C同样很显然 性质不难发现 我在30分钟的时候通过了pretest 但是由于自己的愚蠢 忘记写了一句话 导致FST了。。。

D本来是一个简单的dp题 但是我一直没往dp上想 在网络流上刚了1h之后终于换了思路 在1:45的时候通过了他

然后就时间不多了 E都没看 就去hack 成功hack了2个之后比赛就结束了

 

题解

 

A

如果有两个同样的puppies就符合条件 因为我们可以用这两个把他变成别的颜色 然后就可以一个个把颜色都清除 直到最后剩下一种颜色为止

注意如果长度为1也就是只有1个字符也是可以的 要特判

 

B

我们可以发现如果可行，那么一定有一个质数满足条件

然后我们可以找到$a_1$和$b_1$的所有质因数，分别看他们是否满足条件即可

 

C

假如我们把一个串s分成 s1|s2

那么我们做完操作之后 串变成s1|s2

其中s表示s的倒序

那么我们如果把串写在环上 会发现操作之后整个环没有实质上的

比如串bwbwbwbbwbwb 我们在第4位截开 并操作一番

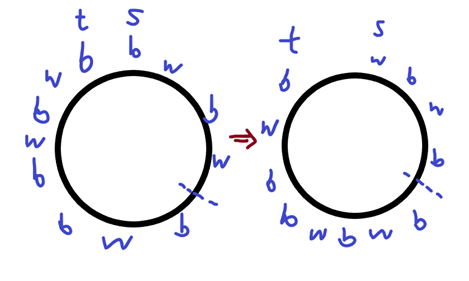
然后我们把第二个环倒置（s到t变成t到s）并且旋转4个位置

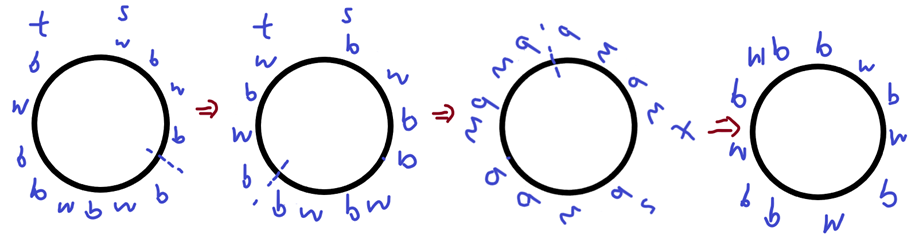
我们得到了原来的环

所以说明了操作不会改变环的实质

所以我们只要计算环上最长的"zebra"长度即可

把串复制一遍 然后扫一遍就可以得到答案

 

D

令$dp1[l][r]$表示从$l$到$r$这一段，以$l-1$为根，能否做成bst

$dp2[l][r]$表示从$l$到$r$这一段，以$r+1$为根，能否做成bst

那么我们这样转移：

$$dp1[l][r]=Or_{k \in (l,r), gcd(a_{l-1},a_k) \gt 1} {dp2[l][k-1] \& dp1[k+1][r]}$$

$$dp2[l][r]=Or_{k \in (l,r), gcd(a_{r+1},a_k) \gt 1} {dp2[l][k-1] \& dp1[k+1][r]}$$

复杂度$O(n^3)$

 

E

想法题

基本的套路是我们找到一个basic state，然后把开始状态和结束状态都转移到basic state

有众多方法 我只讲一个

就是我们把所有designated places都放到第一行上

这是很简单的 我们从上往下，每一行从左往右遍历，然后按照遍历到的顺序把这些格子放到第一行上去

就是第一个遍历到的放到（1,1），第二个遍历到的放到（1,2）……

因为在遍历到一个格子的时候，他前面的格子都被放好了 所以我们可以很轻易的把他放到应该放的位置上

现在我们变成了一个新的问题：两个1*k的序列，我们要通过一些操作变得相同

这也是很简单的

如果总行数只有两行 那么可以手算出来

当总行数超过3行的时候

我们从第一个格子开始 加入他现在在（1，i）要移动到（1，j）

我们把它通过下列操作移动：（1，i），（2，i），……，（2，j），（3，j）

然后我们再把所有第三行上的格子移到第一行

由于移动过程中第二行永远是空或者只有一个格子在移动，所以可行

总操作数：

第一步大概在$n^2$次操作，第二步大概在$n^2$次操作，第三步和第一步一样

所以总操作数大概为$3n^2$

 

F

 

 

G

我们给一个有k个子节点的连通块赋值为$2^k-1$

考察合并操作

我们发现 合并操作前 权值为$2^a-1+2^b-1$

如果把b放到a下面 权值变为$2^{a+1}-1$

如果把a放到b下面 权值变为$2^{b+1}-1$

那么期望权值就是$\frac {2^{a+1}-1} {2} + \frac {2^{b+1}-1} {2}=2^a+2^b-1$

所以总权值+1

那么我们只要算出开始权值和结束权值（就是$2^{n-1}-1$） 他们的差就是答案