【树形DP】codeforces K. Send the Fool Further! (medium)

http://codeforces.com/contest/802/problem/K

【题意】

给定一棵树，Heidi从根结点0出发沿着边走，每个结点最多经过k次，求这棵树的最大花费是多少（同一条边走n次花费只算一次）

【思路】

对于结点v：

• 如果在v的某棵子树停下，那么可以“遍历”k棵子树（有的话）
• 如果还要沿着v返回v的父节点p,那么只能“遍历”k-1棵子树（有的话）。

用dp[v][1]表示第一种情况,dp[v][0]表示第二种情况；最后要求的就是dp[0][0]。

1. 对于dp[v][1]，把所有的子树从大到小排序

(t=k-1)

2. 对于dp[v][0]，枚举子结点dp[u][0]中的u,剩下的k-1个dp[u][1]取最大的，所以我们可以这样预处理：

sum=

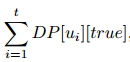(t=k)

• 如果u<k，则target=sum-dp[u][1]+dp[u][0]
• 否则，        target=sum-dp[t][1]+dp[u][0]（t是从大到小排序后的第k-1个）

这样，dp[0][0]就是所求结果（dp[0][0]一定大于dp[0][1]）,时间复杂度是O(nlogn)

【官方题解】

【Accepted】

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<string>
 #include<cmath>
 #include<vector>
 #include<algorithm>

 using namespace std;
 int n,m;
 vector< vector< pair<int,int> > > g;
 const int maxn=1e5+;
 int dp[maxn][];
 void dfs(int v,int p,int edge)
 {
     //从p到v的花费要算在v里
     dp[v][]+=edge;
     dp[v][]+=edge;
     vector< pair<int,int> > s;
     //只有根结点没有父节点，非根结点有父节点，减去1
     if(v==)
     {
         s.resize(g[v].size());
     }
     else
     {
         s.resize(g[v].size()-);
     }
     //遍历
     int num=;
     for(int i=;i<g[v].size();i++)
     {
         int to=g[v][i].first;
         if(to==p)
         {
             continue;
          }
         dfs(to,v,g[v][i].second);
         s[num++]={dp[to][],to};
     }
     //从大到小排序
     sort(s.begin(),s.end());
     reverse(s.begin(),s.end());
     //要记录各个子结点的rank，后面dp[v][0]枚举u是要分类
     int pos[maxn];
     for(int i=;i<s.size();i++)
     {
         pos[s[i].second]=i;
     }
     //计算dp[v][1]
     for(int i=;i<min(m-,(int)s.size());i++)
     {
         dp[v][]+=s[i].first;
     }
     //计算dp[v][0]
     int sum=;
     for(int i=;i<min(m,(int)s.size());i++)
     {
         sum+=s[i].first;
     }
     int maxu=-;
     //枚举
     for(int i=;i<g[v].size();i++)
     {
         int to=g[v][i].first;
         if(to==p)
         {
             continue;
         }
         if(pos[to]<m)
         {
             maxu=max(maxu,sum-dp[to][]+dp[to][]);
         }
         else
         {
             maxu=max(maxu,sum-s[m-].first+dp[to][]);
         }
     }
     if(maxu>-)
     {
         dp[v][]+=maxu;
     }
 }
 int main()
 {
     while(~scanf("%d%d",&n,&m))
     {
         memset(dp,,sizeof(dp));
         g.resize(n);
         int u,v,c;
         for(int i=;i<n-;i++)
         {
             scanf("%d%d%d",&u,&v,&c);
             g[u].push_back({v,c});
             g[v].push_back({u,c});
         }
         //根结点为0,无父结点，根结点到父结点的花费也为0
         dfs(,,);
         printf("%d\n",dp[][]);
     }
     return ;
  }

注意vector开始要resize.....orz

【WA】

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<string>
 #include<algorithm>
 #include<cmath>

 using namespace std;
 int n,k;
 const int maxn=2e5+;
 struct edge
 {
     int to;
     int nxt;
     int c;
 }e[maxn];
 int head[maxn];
 int tot;
 struct node
 {
     int x;
     int id;
 }sz[maxn];
 int rk[maxn];
 bool cmp(node a,node b)
 {
     return a.x>b.x;
 }
 void init()
 {
     memset(head,-,sizeof(head));
     tot=;
 }

 void add(int u,int v,int c)
 {
     e[tot].to=v;
     e[tot].c=c;
     e[tot].nxt=head[u];
     head[u]=tot++;
 }
 int dp[maxn][];

 int dfs(int u,int pa,int c)
 {
     dp[u][]=c;
     dp[u][]=c;
     int cnt=;
     for(int i=head[u];i!=-;i=e[i].nxt)
     {
         int v=e[i].to;
         int c=e[i].c;
         if(v==pa) continue;
         dfs(v,u,c);
         sz[cnt].x=dp[v][];
         sz[cnt++].id=v;
      }
      sort(sz,sz+cnt,cmp);
      for(int i=;i<min(cnt,k-);i++)
      {
          dp[u][]+=sz[i].x;
      }
      int sum=;
      for(int i=;i<min(cnt,k);i++)
      {
          sum+=sz[i].x;
      }
      int ans=;
     for(int i=;i<cnt;i++)
     {
         if(i<k)
         {
             ans=max(ans,sum-sz[i].x+dp[sz[i].id][]);
         }
         else
         {
             ans=max(ans,sum-sz[k-].x+dp[sz[i].id][]);
         }
     }
      dp[u][]+=ans;
 }
 int main()
 {
     while(~scanf("%d%d",&n,&k))
     {
         init();
         memset(dp,,sizeof(dp));
         for(int i=;i<n-;i++)
         {
             int u,v,c;
             scanf("%d%d%d",&u,&v,&c);
             add(u,v,c);
             add(v,u,c);
         }
         dfs(,-,);
         cout<<dp[][]<<endl;
     }
     return ;
 } 

Wrong Answer

终于弄清楚了这个为什么WA!因为我在dfs里用了一个全局变量sz来保存{dp[v][1],v}。然而这是一个全局变量，所以一层里的正确值会被另一层修改！比如当我递归到0时已经有了正确值sz[0].w=5,sz[0].v=2;然而再递归到0的另一分枝1的时候，会修改sz[0],最后再回溯到0时sz[0]已经不是当年的sz[0]了！

所以还是用vector临时申请吧！

【AC（一个更优美的代码）】

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<string>
 #include<algorithm>
 #include<cmath>

 using namespace std;
 int n,k;
 const int maxn=2e5+;
 struct edge
 {
     int to;
     int nxt;
     int c;
 }e[maxn];
 int head[maxn];
 int tot;
 int dp[maxn][];

 struct node
 {
     int x;
     int id;
     node(){}
     node(int _x,int _id):x(_x),id(_id){}
     bool operator<(const node & nd) const
     {
         return x>nd.x;
     }
 };

 void init()
 {
     memset(head,-,sizeof(head));
     tot=;
 }

 void add(int u,int v,int c)
 {
     e[tot].to=v;
     e[tot].c=c;
     e[tot].nxt=head[u];
     head[u]=tot++;
 }

 int dfs(int u,int pa,int c)
 {
     dp[u][]=c;
     dp[u][]=c;
     vector<node> s;
     for(int i=head[u];i!=-;i=e[i].nxt)
     {
         int v=e[i].to;
         int c=e[i].c;
         if(v==pa) continue;
         dfs(v,u,c);
         s.push_back(node(dp[v][],v));
      }
      sort(s.begin(),s.end());
      int sz=s.size();
      for(int i=;i<min(sz,k-);i++)
      {
          dp[u][]+=s[i].x;
      }
      int sum=;
      for(int i=;i<min(sz,k);i++)
      {
          sum+=s[i].x;
      }
      int ans=;
     for(int i=;i<sz;i++)
     {
         if(i<k)
         {
             ans=max(ans,sum-s[i].x+dp[s[i].id][]);
         }
         else
         {
             ans=max(ans,sum-s[k-].x+dp[s[i].id][]);
         }
     }
      dp[u][]+=ans;
 }
 int main()
 {
     while(~scanf("%d%d",&n,&k))
     {
         init();
         memset(dp,,sizeof(dp));
         for(int i=;i<n-;i++)
         {
             int u,v,c;
             scanf("%d%d%d",&u,&v,&c);
             add(u,v,c);
             add(v,u,c);
         }
         dfs(,-,);
         cout<<dp[][]<<endl;
     }
     return ;
 } 

如果是vector<pair<int,int>> 要从大到小排序，可以先sort(s.begin(),s.end()),再reverse(s.begin(),s.end())