「LibreOJ β Round #3」绯色 IOI（抵达）

【题解】

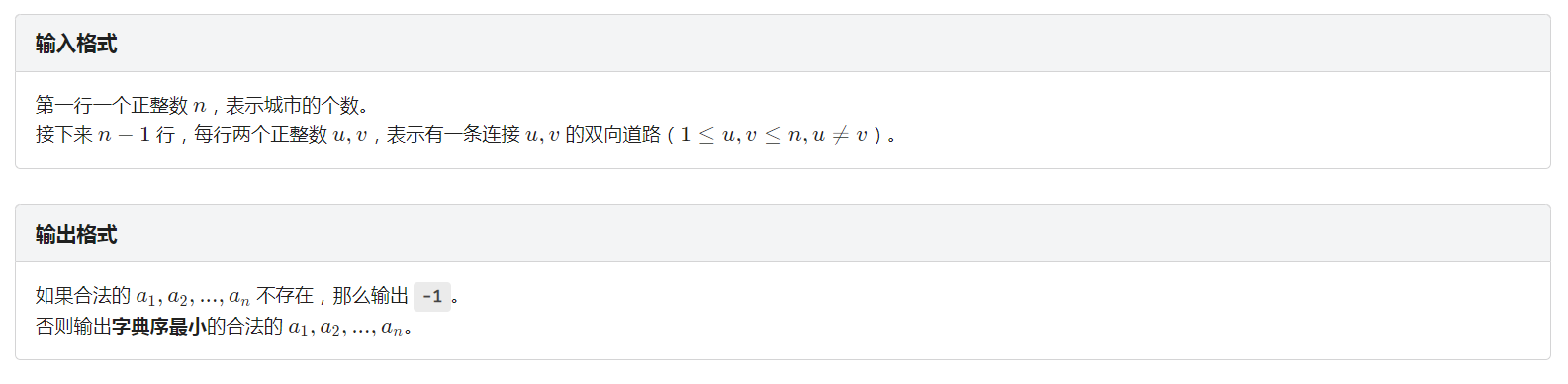
　　我们可以发现叶子节点的关联点一定是它的父亲节点，那么我们dfs一遍就可以求出所有节点的关联点，或者判断出无解。

　　对于每个点i，它的关联点u的危险度肯定比它连接的其他点vi的危险度小，我们从u向vi连边。

　　连边之后我们跑拓扑排序，并且用堆维护当前入度为0的点中编号最小的，以此来让字典序最小。

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<queue>
 #define LL long long
 #define rg register
 #define N 1000010
 using namespace std;
 int n,tot,cnt,last[N],last2[N],link[N],in[N],q[N],ans[N];
 bool vis[N],sol=;
 struct edge{int to,pre;}e[N<<],e2[N<<];
 priority_queue<int,vector<int>,greater<int> >f;
 char buf[],*ptr=buf-;
 inline int read(){
     int f=,k=; char c=*++ptr;
     while(c<'' || c>'') c=='-'&&(f=-), c=*++ptr;
     while(c<='' && c>='') k=k*+c-'', c=*++ptr;
     return k*f;
 }
 void dfs(int x,int fa){
     if(!sol) return;
     bool ok=;
     for(rg int i=last[x],to;i;i=e[i].pre)if((to=e[i].to)!=fa){
         dfs(to,x); if(!vis[to]) link[x]=to,vis[to]=,ok=;
     }
     if(!ok){
         if(vis[fa]) sol=;
         else link[x]=fa,vis[fa]=;
     }
 }
 void dfs2(int x,int fa){
     int u=link[x];
     for(rg int i=last[x],to;i;i=e[i].pre)if((to=e[i].to)!=link[x]){
         in[to]++;
         e2[++tot]=(edge){to,last2[u]}; last2[u]=tot;
 //        printf("%d-->%d\n",u,to);
     }
     for(rg int i=last[x],to;i;i=e[i].pre)if((to=e[i].to)!=fa) dfs2(to,x);
 }
 int main(){
 //    freopen("minecraft.in","r",stdin);
 //    freopen("minecraft.out","w",stdout);
     fread(buf, , sizeof(buf), stdin);
     n=read();
     for(rg int i=;i<n;i++){
         int u=read(),v=read();
         e[++tot]=(edge){v,last[u]}; last[u]=tot;
         e[++tot]=(edge){u,last[v]}; last[v]=tot;
     }
     vis[]=;
     dfs(,);
     if(!sol){puts("-1"); return ;}
 //    for(rg int i=1;i<=n;i++) printf("%d ",link[i]); puts("link");
     tot=;
     dfs2(,);
 //    for(rg int i=1;i<=n;i++) printf("%d ",in[i]); puts("in");
     for(rg int i=;i<=n;i++)if(!in[i]){
         f.push(i);
     }
     while(f.size()){
         int now=f.top(); f.pop();
         ans[++cnt]=now;
         for(rg int i=last2[now],to;i;i=e2[i].pre){
             in[to=e2[i].to]--;
             if(!in[to]) f.push(to);
         }
     }
     for(rg int i=;i<=n;i++) printf("%d ",ans[i]);
     return ;
 }

做法二：

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<queue>
 #define LL long long
 #define rg register
 #define N 500010
 using namespace std;
 int n,m,tot,ans[N],last[N],deg[N];
 bool vis[N],cut[N<<];
 struct edge{
     int to,pre;
 }e[N<<];
 priority_queue<int,vector<int>,greater<int> >q;
 inline int read(){
     int k=,f=; char c=getchar();
     while(c<''||c>'')c=='-'&&(f=-),c=getchar();
     while(''<=c&&c<='')k=k*+c-'',c=getchar();
     return k*f;
 }
 int main(){
     n=read(); tot=;
     if(n==) return puts("-1"),;
     for(rg int i=;i<n;i++){
         int u=read(),v=read();
         e[++tot]=(edge){u,last[v]}; last[v]=tot;
         e[++tot]=(edge){v,last[u]}; last[u]=tot;
         deg[u]++; deg[v]++;
     }
     for(rg int i=;i<=n;i++)if(deg[i]<=) q.push(i),vis[i]=;
     for(rg int t=,now;t<=n;t++){
         if(!q.size()){puts("-1"); return ;}
         ans[t]=now=q.top(); q.pop();
         for(rg int i=last[now],to;i;i=e[i].pre)if(!cut[i]){
             to=e[i].to;
             for(rg int j=last[to],to2;j;j=e[j].pre){
                 deg[to2=e[j].to]--;
                 if(!vis[to2]&&deg[to2]<=) q.push(to2),vis[to2]=;
                 cut[j^]=;
             }
         }
     }
     for(rg int i=;i<=n;i++) printf("%d ",ans[i]);
     return ;
 }