网络流之最大流算法(EK算法和Dinc算法）

最大流

网络流的定义：

在一个网络(有流量）中有两个特殊的点，一个是网络的源点（s），流量只出不进，一个是网络的汇点(t),流量只进不出。

最大流：就是求s-->t的最大流量

假设 u,v 两个点，连接这两个点的边为e(u,v);

对于每一条边都有一个实际流量f(u,v),还有一个容量c(u,v),就是这条边上可以通过的最大流量。

当一条边的容量c(u,v)=0,证明这条边是不存在的，

作为一个合格的网络流，必须满足三个条件：

1>每条边的实际流量小于等于容量  f(u,v)<=c(u,v);

2>f(u,v)=-f(v,u);

3>对于不是源点和汇点的点，流入的流量等于流出的流量

如何来求一个网络的最大流：

如图是一个网路流，很明显看出答案是4。

我们要求s-t的流量，我们可以选择这样来求解，我们先从s点出发，找到一条s-t的路径，记录这条路径上那个最小的实际流量，

算法就是我们要找到很多条这样的路径，但这些路径都应该是不同的，所有我们只需要把这多条路径的的最小流量相加 得到就是最大流、

这个寻找s-t的路径也叫做增广路算法。

其实这里困难的就是如何保证这些路径是不会相同的 这是涉及到一个概念 就是残留网络

残留网络就是每次利用增广路算法找到这条路径的最小实际流量 minn，我们在原网络中把这条边的容量都减去minn，所以必定这条路径中一定会有流量为0。

所有下次增广的话，就一定不会走原路 因为这条路径中有边的流量有0，走是没有意义的。一直到不能增广为止，得到的和就是最大流

如上图 我们可以很好的求出最大流

先增广 找到 s-1-t 这条路 minn=2 所以他的残留网络图变为

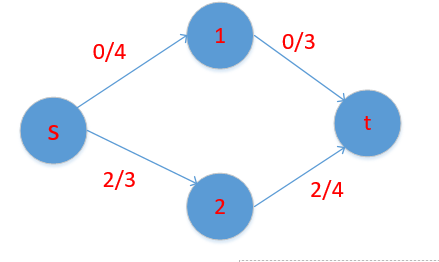
继续增广，得的残留网络为：

这样很容易求到最大流，但这种其实是错误的，比如我们换一个图

假设我们先增广  s-1-2-t,  其实我们就只不在增广了，结果等于2，其实这答案是4，这里就要体现反向边的作用了

我们最开始设的  反向边的值都是0的，就是我们在每次增广后的残流网络不仅边的流量要减去minn，反向弧的流量应该加上minn

比如 ，你先增广s-1-2-t  残留网络为

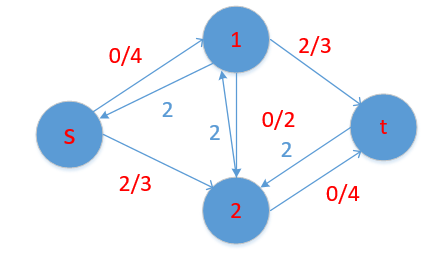
这样我们依然可以继续增广，最终可以得到答案为4

就是给了一个反悔的机会，就是比如我有这条的反向边我依然不能增广，哪这就是无所谓的额，

当我们第二次的增广路走2-1这条反向边的时候，就相当于把1-2这条正向边已经是用了的流量给”退”了回去，不走1-2这条路，而改走从1点出发的其他的路也就是1-t。 （有人问如果这里没有1-t怎么办，这时假如没有1-t这条路的话，最终这条增广路也不会存在，因为他根本不能走到汇点）

同时本来在2-t上的流量由s-2-t这条路来”接管”.

这是就网络流最大流中最简单的一个EK算法了(全名不记得了）

下面给出一道入门题   hdu  3549

Flow Problem

Time Limit: 5000/5000 MS (Java/Others)    Memory Limit: 65535/32768 K (Java/Others)
Total Submission(s): 16416    Accepted Submission(s): 7747

Problem Description

Network
flow is a well-known difficult problem for ACMers. Given a graph, your
task is to find out the maximum flow for the weighted directed graph.

Input

The first line of input contains an integer T, denoting the number of test cases.
For
each test case, the first line contains two integers N and M, denoting
the number of vertexes and edges in the graph. (2 <= N <= 15, 0
<= M <= 1000)
Next M lines, each line contains three integers
X, Y and C, there is an edge from X to Y and the capacity of it is C. (1
<= X, Y <= N, 1 <= C <= 1000)

Output

For each test cases, you should output the maximum flow from source 1 to sink N.

Sample Input

2

3 2

1 2 1

2 3 1

3 3

1 2 1

2 3 1

1 3 1

Sample Output

Case 1:

1
Case 2: 2

Author

HyperHexagon

Source

HyperHexagon's Summer Gift (Original tasks)

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<cstdlib>
 #include<string.h>
 #include<set>
 #include<vector>
 #include<queue>
 #include<stack>
 #include<map>
 #include<cmath>
 typedef long long ll;
 typedef unsigned long long LL;
 using namespace std;
 const double PI=acos(-1.0);
 const double eps=0.0000000001;
 const int INF=1e9;
 const int N=+;
 int mp[N][N];
 int vis[N];
 int pre[N];
 int m,n;
 int BFS(int s,int t){
     queue<int>q;
     memset(pre,-,sizeof(pre));
     memset(vis,,sizeof(vis));
     pre[s]=;
     vis[s]=;
     q.push(s);
     while(!q.empty()){
         int p=q.front();
         q.pop();
         for(int i=;i<=m;i++){
             if(mp[p][i]>&&vis[i]==){
                 pre[i]=p;
                 vis[i]=;
                 if(i==t)return ;
                 q.push(i);
             }
         }
     }
     return false;
 }
 int EK(int s,int t){
     int flow=;
     //cout<<BFS(s,t)<<endl;
     while(BFS(s,t)){
         //BFS(s,t);
         int dis=INF;
         for(int i=t;i!=s;i=pre[i])
             dis=min(mp[pre[i]][i],dis);
         for(int i=t;i!=s;i=pre[i]){
             mp[pre[i]][i]=mp[pre[i]][i]-dis;
             mp[i][pre[i]]=mp[i][pre[i]]+dis;
         }
         flow=flow+dis;
     }
     return flow;
 }
 int main(){
     int Case;
     cin>>Case;
     int tt=;
     while(Case--){
        scanf("%d%d",&m,&n);
         memset(mp,,sizeof(mp));
         for(int i=;i<n;i++){
             int u,v,w;
             scanf("%d%d%d",&u,&v,&w);
             mp[u][v]=w+mp[u][v];
            // mp[v][u]=0;
         }
         int ans=EK(,m);
         cout<<"Case "<<tt++<<":"<<" ";
         cout<<ans<<endl;
     }

 }

由于EK算法容易超时  所有这个在比赛中不怎么用  所以我们就需要复杂度低的  接下来我们就介绍Dinc算法

其实Dinc算法和EK是很相似的，Dinc中有一个概念  叫做层次图，就是这个使其复杂度低了很多的，主要就是一个多路增广，

就是在BFS一遍的过程中都达到多路增广，而减少复杂度

如下图

Dinc的写法 也是一个板子

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<cstdlib>
 #include<string.h>
 #include<set>
 #include<vector>
 #include<queue>
 #include<stack>
 #include<map>
 #include<cmath>
 typedef long long ll;
 typedef unsigned long long LL;
 using namespace std;
 const double PI=acos(-1.0);
 const double eps=0.0000000001;
 const int INF=1e9;
 const int N=+;
 int head[N];
 int dis[N];
 int tot;
 int n,m;
 struct node{
     int to,next,flow;
 }edge[N<<];
 void init(){
     memset(head,-,sizeof(head));
     tot=;
 }
 void add(int u,int v,int c){
     edge[tot].to=v;
     edge[tot].flow=c;
     edge[tot].next=head[u];
     head[u]=tot++;
 }
 int BFS(int s,int t){
     queue<int>q;
     memset(dis,-,sizeof(dis));
     q.push(s);
     dis[s]=;
     while(!q.empty()){
         int x=q.front();
         q.pop();
         if(x==t)return ;
         for(int i=head[x];i!=-;i=edge[i].next){
             int v=edge[i].to;
             if(edge[i].flow&&dis[v]==-){
                 dis[v]=dis[x]+;
                 q.push(v);
             }
         }
     }
     if(dis[t]==-)return ;
     else
         return ;
 }
 int DFS(int s,int flow){
     if(s==m)return flow;
     int ans=;
     for(int i=head[s];i!=-;i=edge[i].next){
         int v=edge[i].to;
         if(edge[i].flow&&dis[v]==dis[s]+){
             int f=DFS(v,min(flow-ans,edge[i].flow));
             edge[i].flow-=f;
             edge[i^].flow+=f;
             ans+=f;
             if(ans==flow)return ans;
         }
     }
     return ans;
 }
 int Dinc(int s,int t){
     int flow=;
     while(BFS(s,t)){
         flow+=DFS(s,INF);
     }
     return flow;
 }
 int main(){
     int Case;
     scanf("%d",&Case);
     int tt=;
     while(Case--){
         init();
         scanf("%d%d",&m,&n);
         for(int i=;i<n;i++){
             int u,v,w;
             scanf("%d%d%d",&u,&v,&w);
             add(u,v,w);
             add(v,u,);
            // mp[v][u]=0;
         }
         int ans=Dinc(,m);
         cout<<"Case "<<tt++<<":"<<" ";
         cout<<ans<<endl;
     }

 }