Codeforces Round #319 (Div. 1) C. Points on Plane 分块

C. Points on Plane

Time Limit: 1 Sec

Memory Limit: 256 MB

题目连接

http://codeforces.com/contest/576/problem/C

Description

On a plane are n points (xi, yi) with integer coordinates between 0 and 106. The distance between the two points with numbers a and bis said to be the following value: 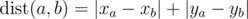 (the distance calculated by such formula is called Manhattan distance).

We call a hamiltonian path to be some permutation pi of numbers from 1 to n. We say that the length of this path is value .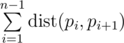

Find some hamiltonian path with a length of no more than 25 × 108. Note that you do not have to minimize the path length.

Input

The first line contains integer n (1 ≤ n ≤ 106).

The i + 1-th line contains the coordinates of the i-th point: xi and yi (0 ≤ xi, yi ≤ 106).

It is guaranteed that no two points coincide.

Output

Print the permutation of numbers pi from 1 to n — the sought Hamiltonian path. The permutation must meet the inequality .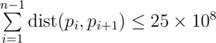

If there are multiple possible answers, print any of them.

It is guaranteed that the answer exists.

Sample Input

5
0 7
8 10
3 4
5 0
9 12

Sample Output

4 3 1 2 5

HINT

In the sample test the total distance is:

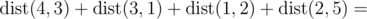
(|5 - 3| + |0 - 4|) + (|3 - 0| + |4 - 7|) + (|0 - 8| + |7 - 10|) + (|8 - 9| + |10 - 12|) = 2 + 4 + 3 + 3 + 8 + 3 + 1 + 2 = 26

题意

给你一个曼哈顿距离的图，然后要求你找到一个链，链穿了所有的点

然后要求这链的长度<=25*10e8

题解：

就分块咯，分成1000块，每个块内y坐标最多走10e6长度，x坐标最多走n*10e3个，n表示一块内的点数

n是一个二次函数维护的东西……所以大概答案最后就是10e3(10e6+10e6) = 2*10e9

所以大概看看脸，就能把这道题AC了

代码：

//qscqesze
#include <cstdio>
#include <cmath>
#include <cstring>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <set>
#include <bitset>
#include <vector>
#include <sstream>
#include <queue>
#include <typeinfo>
#include <fstream>
#include <map>
#include <stack>
typedef long long ll;
using namespace std;
//freopen("D.in","r",stdin);
//freopen("D.out","w",stdout);
#define sspeed ios_base::sync_with_stdio(0);cin.tie(0)
#define maxn 1000500
#define mod 1001
#define eps 1e-9
#define pi 3.1415926
int Num;
//const int inf=0x7fffffff;
const ll inf=;
inline ll read()
{
    ll x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
//*************************************************************************************

pair<int,pair<int,int> > p[maxn];

int main()
{
    int n=read();
    for(int i=;i<n;i++)
    {
        p[i].first = read();p[i].first/=;
        p[i].second.first = read();p[i].second.second = i;
    }
    sort(p,p+n);
    for(int i=;i<n;i++)
        printf("%d ",p[i].second.second+);
}