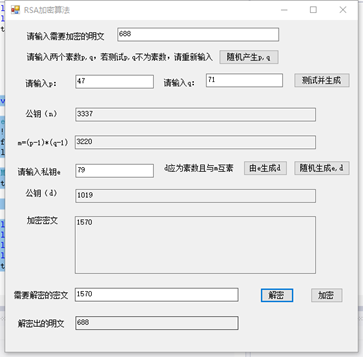
RSA加密算法验证（C#实现）

RSA算法简单原理介绍（节选于网络）

假设Alice想要通过一个不可靠的媒体接收Bob的一条私人讯息。她可以用以下的方式来产生一个公钥和一个私钥：

1. 随意选择两个大的质数p和q，p不等于q，计算N=pq。
2. 根据欧拉函数，求得r = (p-1)(q-1)
3. 选择一个小于 r 的整数 e，求得 e 关于模 r 的模反元素，命名为d。（模反元素存在，当且仅当e与r互质）
4. 将 p 和 q 的记录销毁。

(N,e)是公钥，(N,d)是私钥。Alice将她的公钥(N,e)传给Bob，而将她的私钥(N,d)藏起来。

加密消息

　　假设Bob想给Alice送一个消息m，他知道Alice产生的N和e。他使用起先与Alice约好的格式将m转换为一个小于N的整数n，比如他可以将每一个字转换为这个字的Unicode码，然后将这些数字连在一起组成一个数字。假如他的信息非常长的话，他可以将这个信息分为几段，然后将每一段转换为n。用下面这个公式他可以将n加密为c：

　　ne ≡ c (mod N)

计算c并不复杂。Bob算出c后就可以将它传递给Alice。

解密消息

Alice得到Bob的消息c后就可以利用她的密钥d来解码。她可以用以下这个公式来将c转换为n：

　　cd ≡ n (mod N)

得到n后，她可以将原来的信息m重新复原。

解码的原理是：

　　cd ≡ n e·d(mod N)

以及ed ≡ 1 (mod p-1)和ed ≡ 1 (mod q-1)。由费马小定理可证明（因为p和q是质数）

　　n e·d ≡ n (mod p) 　　和 　n e·d ≡ n (mod q)

这说明（因为p和q是不同的质数，所以p和q互质）

　　n e·d ≡ n (mod pq)

 using System;
 using System.Collections.Generic;
 using System.ComponentModel;
 using System.Data;
 using System.Drawing;
 using System.Linq;
 using System.Text;
 using System.Threading.Tasks;
 using System.Windows.Forms;

 namespace RSA
 {
     public partial class Form1 : Form
     {
         public Form1()
         {
             InitializeComponent();
         }

         //****************************************
         //验证输入的p,q是否为素数，并计算n与m
         //****************************************
         private void button1_Click(object sender, EventArgs e)
         {
             long p, q;
             //获取p,q的值
             p = long.Parse(textBox1.Text);
             q = long.Parse(textBox2.Text);

             //判断p，q是否为素数，若为真进行计算，则否弹出提示
             if (isPrim(p) && isPrim(q))
             {
                 long n = p * q;
                 long m = (p - ) * (q - );
                 textBox3.Text = n.ToString();
                 textBox4.Text = m.ToString();
             }
             else
             {
                 MessageBox.Show("请按要求,重新输入p,q");
                 textBox1.Clear();
                 textBox2.Clear();
                 textBox3.Clear();
                 textBox1.Focus();
             }

         }

         //****************************************
         //用随机数生成素数pq，并计算n与m
         //****************************************

         private void button5_Click(object sender, EventArgs e)
         {
             //生成随机数工具
             Random random = new Random();
             long p, q;

             //设置判断标志
             Boolean flag = false;
             while (!flag)
             {
                 p = random.Next();
                 q = random.Next();

                 //若生成的两个随机数都为素数，设定更新标志，并进行显示
                 if (isPrim(p) && isPrim(q))
                 {
                     flag = true;
                     textBox1.Text = p.ToString();
                     textBox2.Text = q.ToString();
                     textBox3.Clear();
                     textBox4.Clear();
                 }

             }
         }

         //****************************************
         //验证输入的d是否为素数， 并计算公钥d
         //****************************************
         private void button2_Click(object sender, EventArgs e)
         {
             //获取d,m的值
             long d = long.Parse(textBox5.Text);
             long m = long.Parse(textBox4.Text);

             //判断输入的d是否符合条件
             if (d >  && d < m && gcd(d, m) ==  && isPrim(d))
             {
                 //使用逆元函数，计算d,m的逆元
                 long result = niyuan(d, m);
                 textBox6.Text = result.ToString();
             }
             else
             {
                 MessageBox.Show("输入的 e 不符合要求，请按要求,重新输入公钥 e ！");
                 textBox5.Clear();
                 textBox5.Focus();

             }
         }

         //****************************************
         //随机生成私钥d，并计算出公钥e
         //****************************************
         private void button6_Click(object sender, EventArgs e)
         {
             long d = ;

             //获取m的值，用以计算e
             long m = long.Parse(textBox4.Text);

             //生成随机数工具，并设置随机是否完成标志
             Random radom = new Random();
             Boolean flag = false;
             while(!flag)
             {
                  d = radom.Next();
                  if (d >  && d < m && gcd(d, m) ==  && isPrim(d))
                  {
                       flag = true;
                  }
             }

             //利用逆元函数计算公钥
             long result = niyuan(d, m);

             textBox5.Text = d.ToString();
             textBox6.Text = result.ToString();

         }

         //****************************************
         //利用公钥n和私钥e，加密明文
         //****************************************
         private void button4_Click(object sender, EventArgs e)
         {
             //设置标志，判断是否已经输入明文
             Boolean flag = false;
             if (!string.IsNullOrWhiteSpace(textBox7.Text))
                 flag = true;

             if(flag == false)
             {
                 MessageBox.Show("加密前,请先输入明文！");
                 textBox7.Focus();
             }
             else
             {
                 long n = long.Parse(textBox3.Text);
                 long m = long.Parse(textBox7.Text);
                 long E = long.Parse(textBox5.Text);

                 //利用快速指数模运算函数生成密文
                 long C = getMod(E, m, n);
                 textBox8.Text = C.ToString();
             }

          }

         //****************************************
         //利用公钥n和公钥d，解密密文
         //****************************************
         private void button3_Click(object sender, EventArgs e)
         {
             //设置标志，判断是否已经输入密文
             Boolean flag = false;
             if (!string.IsNullOrWhiteSpace(textBox9.Text))
                 flag = true;
             if(flag == false)
             {
                 MessageBox.Show("解密前，请先输入密文！");
                 textBox9.Focus();
             }
             else
             {
                 long C = long.Parse(textBox9.Text);
                 long n = long.Parse(textBox3.Text);
                 long d = long.Parse(textBox6.Text);

                 //利用快速指数模运算函数解密密文
                 long M = getMod(d, C, n);
                 textBox10.Text = M.ToString();
             }

         }

         //****************************************
         //输入一个数，以6为步进单元判断其是否为素数
         //****************************************
         private bool isPrim(long num)
         {
             //两个较小数另外处理
             if (num ==  || num == )
                 return true;
             //不在6的倍数两侧的一定不是质数
             if (num %  !=  && num %  != )
                 return false;
             long tmp = (long)Math.Sqrt(num);
             //在6的倍数两侧的也可能不是质数
             for (long i = ; i <= tmp; i += )
                 if (num % i ==  || num % (i + ) == )
                     return false;
             //排除所有，剩余的是质数
             return true;
         }

         //****************************************
         //采用递归的形式，判断两个数是否互质
         //****************************************
         private long gcd(long x, long y)
         {
             return y !=  ? gcd(y, x % y) : x;
         }

         //****************************************
         //利用欧几里得算法计算m，d的逆元
         //****************************************
         private long niyuan(long number1, long number3)
         {
             long x1 = , x2 = , x3 = number3, y1 = , y2 = , y3 = number1;
             long q;
             long number4 = ;
             long t1, t2, t3;
             while (y3 != )
             {
                 if (y3 == )
                 {
                     number4 = y2;
                     break;
                 }
                 else
                 {
                     q = (x3 / y3);
                     t1 = x1 - q * y1;
                     t2 = x2 - q * y2;
                     t3 = x3 - q * y3;
                     x1 = y1; x2 = y2; x3 = y3;
                     y1 = t1; y2 = t2; y3 = t3;
                 }
             }
             if (number4 < )
                 number4 = number4 + number3;
             return number4;
         }

         //****************************************
         //利用快速指数模运算，计算m^e mod n
         //****************************************
         private long getMod(long a, long b, long c)
         {
             //指数 e --> a  底数 m --> b   模数 n --> c
             long number3 = ;
             while (a != )
             {
                 if (a %  == )
                 {
                     a = a - ;
                     number3 = (number3 * b) % c;
                 }
                 else
                 {
                     a = (a / );
                     b = (b * b) % c;
                 }
             }
             return number3;

         }
     }
 }