CodeForces 235E Number Challenge (莫比乌斯反演)

题意：求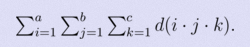，其中d(x) 表示 x 的约数个数。

析：其实是一个公式题，要知道一个结论

知道这个结论就好办了。

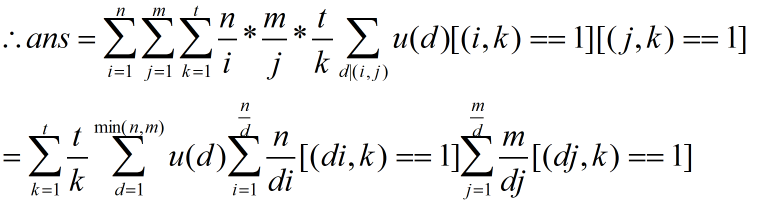
然后就可以解决这个问题了，优化就是记忆化gcd。

代码如下：

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <cstdio>
#include <string>
#include <cstdlib>
#include <cmath>
#include <iostream>
#include <cstring>
#include <set>
#include <queue>
#include <algorithm>
#include <vector>
#include <map>
#include <cctype>
#include <cmath>
#include <stack>
#include <sstream>
#include <list>
#include <assert.h>
#include <bitset>
#include <numeric>
#define debug() puts("++++")
#define gcd(a, b) __gcd(a, b)
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define fi first
#define se second
#define pb push_back
#define sqr(x) ((x)*(x))
#define ms(a,b) memset(a, b, sizeof a)
#define sz size()
#define pu push_up
#define pd push_down
#define cl clear()
#define lowbit(x) -x&x
//#define all 1,n,1
#define FOR(i,x,n)  for(int i = (x); i < (n); ++i)
#define freopenr freopen("in.txt", "r", stdin)
#define freopenw freopen("out.txt", "w", stdout)
using namespace std;

typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> P;
const int INF = 0x3f3f3f3f;
const LL LNF = 1e17;
const double inf = 1e20;
const double PI = acos(-1.0);
const double eps = 1e-8;
const int maxn = 2000 + 1;
const int maxm = 2e4 + 10;
const int mod = 1073741824;
const int dr[] = {-1, 1, 0, 0, 1, 1, -1, -1};
const int dc[] = {0, 0, 1, -1, 1, -1, 1, -1};
const char *de[] = {"0000", "0001", "0010", "0011", "0100", "0101", "0110", "0111", "1000", "1001", "1010", "1011", "1100", "1101", "1110", "1111"};
int n, m;
const int mon[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
const int monn[] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
inline bool is_in(int r, int c) {
  return r >= 0 && r < n && c >= 0 && c < m;
}

bool vis[maxn];
int g[maxn][maxn], mu[maxn], prime[maxn];

void Moblus(){
  mu[1] = 1;  int tot = 0;
  for(int i = 2; i <= n; ++i){
    if(!vis[i])  prime[tot++] = i, mu[i] = -1;
    for(int j = 0; j < tot; ++j){
      int t = i * prime[j];
      if(t > n)  break;
      vis[t] = 1;
      if(i % prime[j] == 0)  break;
      mu[t] = -mu[i];
    }
  }
}

int ggcd(int a, int b){
  if(!b)  return a;
  if(g[a][b])  return g[a][b];
  return g[a][b] = g[b][a] = gcd(b, a%b);
}

int solve(int n, int d, int k){
  int ans = 0;
  for(int i = 1; i <= n; ++i)
    if(ggcd(d*i, k) == 1)  ans += n / i;
  return ans;
}

int main(){
  int t;
  scanf("%d %d %d",  &n, &m, &t);
  if(n > m)  swap(n, m);
  if(n > t)  swap(n, t);
  if(t > m)  swap(m, t);
  Moblus();
  int ans = 0;
  for(int i = 1; i <= t; ++i){
    int tmp = 0;
    for(int j = 1; j <= n; ++j)  if(mu[j])
      tmp += mu[j] * solve(n/j, j, i) * solve(m/j, j, i);
    ans += t/i * tmp;
  }
  printf("%d\n", (ans%mod+mod)%mod);
  return 0;
}