IntelliJ IDEA2018.1、2017.3激活

IntelliJ IDEA2018.1、2017.3破解教程

http://idea.java.sx/

简单快捷！！

———————————————————————————————————————— 
由于JetBrains封杀，大部分激活服务器已经不能使用，如果以上方法无效，则可以使用下面的比较麻烦的方法，但是有效期是到December 31，2099（emmmm，也算是永久破解了吧，毕竟是到2099年）

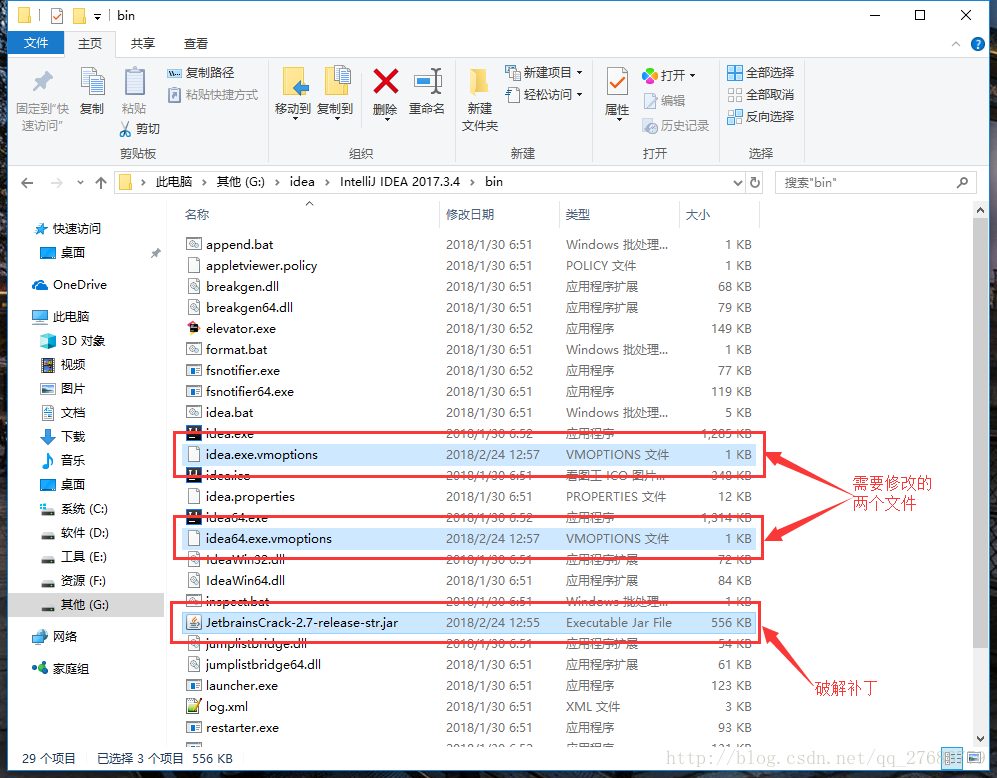
（1）下载破解补丁 
把下载的破解补丁放在你的idea的安装目录下的bin的目录下面（如下图所示），本文示例为G:\idea\IntelliJ IDEA 2017.3.4 
破解补丁下载：http://idea.lanyus.com/jar/JetbrainsCrack-2.7-release-str.jar

（2）修改配置文件 
打开并编辑 idea.exe.vmoptions和idea64.exe.vmoptions这两个文件（使用记事本、ultraedit或notepad++等编辑器打开），在上述两个文件的最后一行均加上下面这段代码 
-javaagent:G:\idea\IntelliJ IDEA 2017.3.4\bin\JetbrainsCrack-2.7-release-str.jar（注意：不要忘记修改成你自己idea的安装目录和对应的jar的版本）

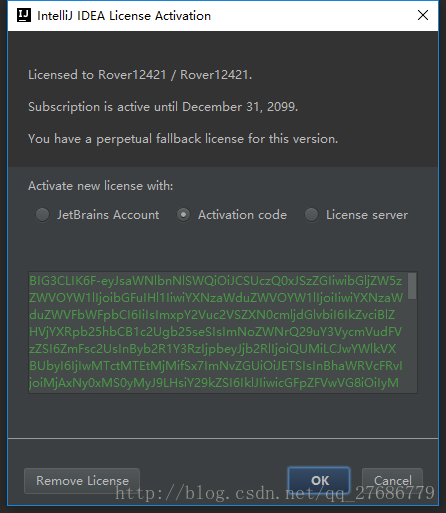
（3）输入激活码 
启动idea，选择Activation Code，并输入如下激活码： 

BIG3CLIK6F-eyJsaWNlbnNlSWQiOiJCSUczQ0xJSzZGIiwibGljZW5zZWVOYW1lIjoibGFuIHl1IiwiYXNzaWduZWVOYW1lIjoiIiwiYXNzaWduZWVFbWFpbCI6IiIsImxpY2Vuc2VSZXN0cmljdGlvbiI6IkZvciBlZHVjYXRpb25hbCB1c2Ugb25seSIsImNoZWNrQ29uY3VycmVudFVzZSI6ZmFsc2UsInByb2R1Y3RzIjpbeyJjb2RlIjoiQUMiLCJwYWlkVXBUbyI6IjIwMTctMTEtMjMifSx7ImNvZGUiOiJETSIsInBhaWRVcFRvIjoiMjAxNy0xMS0yMyJ9LHsiY29kZSI6IklJIiwicGFpZFVwVG8iOiIyMDE3LTExLTIzIn0seyJjb2RlIjoiUlMwIiwicGFpZFVwVG8iOiIyMDE3LTExLTIzIn0seyJjb2RlIjoiV1MiLCJwYWlkVXBUbyI6IjIwMTctMTEtMjMifSx7ImNvZGUiOiJEUE4iLCJwYWlkVXBUbyI6IjIwMTctMTEtMjMifSx7ImNvZGUiOiJSQyIsInBhaWRVcFRvIjoiMjAxNy0xMS0yMyJ9LHsiY29kZSI6IlBTIiwicGFpZFVwVG8iOiIyMDE3LTExLTIzIn0seyJjb2RlIjoiREMiLCJwYWlkVXBUbyI6IjIwMTctMTEtMjMifSx7ImNvZGUiOiJEQiIsInBhaWRVcFRvIjoiMjAxNy0xMS0yMyJ9LHsiY29kZSI6IlJNIiwicGFpZFVwVG8iOiIyMDE3LTExLTIzIn0seyJjb2RlIjoiUEMiLCJwYWlkVXBUbyI6IjIwMTctMTEtMjMifSx7ImNvZGUiOiJDTCIsInBhaWRVcFRvIjoiMjAxNy0xMS0yMyJ9XSwiaGFzaCI6IjQ3NzU1MTcvMCIsImdyYWNlUGVyaW9kRGF5cyI6MCwiYXV0b1Byb2xvbmdhdGVkIjpmYWxzZSwiaXNBdXRvUHJvbG9uZ2F0ZWQiOmZhbHNlfQ==-iygsIMXTVeSyYkUxAqpHmymrgwN5InkOfeRhhPIPa88FO9FRuZosIBTY18tflChACznk3qferT7iMGKm7pumDTR4FbVVlK/3n1ER0eMKu2NcaXb7m10xT6kLW1Xb3LtuZEnuis5pYuEwT1zR7GskeNWdYZ0dAJpNDLFrqPyAPo5s1KLDHKpw+VfVd4uf7RMjOIzuJhAAYAG+amyivQt61I9aYiwpHQvUphvTwi0X0qL/oDJHAQbIv4Qwscyo4aYZJBKutYioZH9rgOP6Yw/sCltpoPWlJtDOcw/iEWYiCVG1pH9AWjCYXZ9AbbEBOWV71IQr5VWrsqFZ7cg7hLEJ3A==-MIIEPjCCAiagAwIBAgIBBTANBgkqhkiG9w0BAQsFADAYMRYwFAYDVQQDDA1KZXRQcm9maWxlIENBMB4XDTE1MTEwMjA4MjE0OFoXDTE4MTEwMTA4MjE0OFowETEPMA0GA1UEAwwGcHJvZDN5MIIBIjANBgkqhkiG9w0BAQEFAAOCAQ8AMIIBCgKCAQEAxcQkq+zdxlR2mmRYBPzGbUNdMN6OaXiXzxIWtMEkrJMO/5oUfQJbLLuMSMK0QHFmaI37WShyxZcfRCidwXjot4zmNBKnlyHodDij/78TmVqFl8nOeD5+07B8VEaIu7c3E1N+e1doC6wht4I4+IEmtsPAdoaj5WCQVQbrI8KeT8M9VcBIWX7fD0fhexfg3ZRt0xqwMcXGNp3DdJHiO0rCdU+Itv7EmtnSVq9jBG1usMSFvMowR25mju2JcPFp1+I4ZI+FqgR8gyG8oiNDyNEoAbsR3lOpI7grUYSvkB/xVy/VoklPCK2h0f0GJxFjnye8NT1PAywoyl7RmiAVRE/EKwIDAQABo4GZMIGWMAkGA1UdEwQCMAAwHQYDVR0OBBYEFGEpG9oZGcfLMGNBkY7SgHiMGgTcMEgGA1UdIwRBMD+AFKOetkhnQhI2Qb1t4Lm0oFKLl/GzoRykGjAYMRYwFAYDVQQDDA1KZXRQcm9maWxlIENBggkA0myxg7KDeeEwEwYDVR0lBAwwCgYIKwYBBQUHAwEwCwYDVR0PBAQDAgWgMA0GCSqGSIb3DQEBCwUAA4ICAQC9WZuYgQedSuOc5TOUSrRigMw4/+wuC5EtZBfvdl4HT/8vzMW/oUlIP4YCvA0XKyBaCJ2iX+ZCDKoPfiYXiaSiH+HxAPV6J79vvouxKrWg2XV6ShFtPLP+0gPdGq3x9R3+kJbmAm8w+FOdlWqAfJrLvpzMGNeDU14YGXiZ9bVzmIQbwrBA+c/F4tlK/DV07dsNExihqFoibnqDiVNTGombaU2dDup2gwKdL81ua8EIcGNExHe82kjF4zwfadHk3bQVvbfdAwxcDy4xBjs3L4raPLU3yenSzr/OEur1+jfOxnQSmEcMXKXgrAQ9U55gwjcOFKrgOxEdek/Sk1VfOjvS+nuM4eyEruFMfaZHzoQiuw4IqgGc45ohFH0UUyjYcuFxxDSU9lMCv8qdHKm+wnPRb0l9l5vXsCBDuhAGYD6ss+Ga+aDY6f/qXZuUCEUOH3QUNbbCUlviSz6+GiRnt1kA9N2Qachl+2yBfaqUqr8h7Z2gsx5LcIf5kYNsqJ0GavXTVyWh7PYiKX4bs354ZQLUwwa/cG++2+wNWP+HtBhVxMRNTdVhSm38AknZlD+PTAsWGu9GyLmhti2EnVwGybSD2Dxmhxk3IPCkhKAK+pl0eWYGZWG3tJ9mZ7SowcXLWDFAk0lRJnKGFMTggrWjV8GYpw5bq23VmIqqDLgkNzuoog==

• 1

（4）激活成功！

原文；https://blog.csdn.net/qq_27686779/article/details/78870816