INDEX--从数据存放的角度看索引2

在上次<INDEX--从数据存放的角度看索引>中，我们说到"唯一非聚集索引"和“非唯一非聚集索引”在存储上有一个明显的差别：唯一非聚集索引的非叶子节点上不会包含RID的数据，让我们继续来深挖一下。

准备测试数据：

CREATE TABLE TB1
(
    C1 INT,
    C2 INT,
    C3 INT
)
GO
CREATE UNIQUE CLUSTERED INDEX IDX_C1 ON TB1(C1)
GO
CREATE UNIQUE INDEX IDX_C2 ON TB1(C2)
GO
CREATE INDEX IDX_C3 ON TB1(C3)
GO
INSERT INTO TB1(C1,C2,C3)VALUES(1,1,1)
GO
INSERT INTO TB1(C1,C2,C3)VALUES(2,2,2)
GO
INSERT INTO TB1(C1,C2,C3)VALUES(3,3,3)

索引编号如下：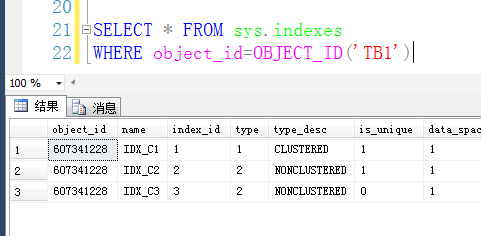

再通过DBCC IND和DBCC PAGE来查看页情况

唯一非聚集索引IDX_C2的数据页：

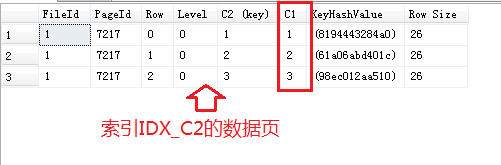
非唯一非聚集索引IDX_C3的数据页：

以上两张图有个明显的区别是C1和C1(key)，难道在“非唯一非聚集索引”中，“聚集索引键”也被放到“非聚集索引键”中并且参与排序啦？

相信很多DBA的朋友都遇到这样的问题，要按照某些状态值来查找数据，而这些状态值是一个很小的集合(数量很小)，如查找状态值为1的最大订单号

SELECT TOP(1)*
FROM dbo.Orders
WHERE OrderState=1
ORDER BY OrderID DESC 

虽然OrderID为主键和唯一聚集索引，但按照OrderID来查找，可能需要进行大范围CLUSTERED INDEX SEEK才能找到满足条件OrderState=1的数据，因此尽管OrderState的可选择性较低，我们还是会对其建立索引，那么问题来了？我们索引该建成什么样呢？
是建成：

CREATE INDEX IDX_OrderState
ON dbo.Orders
(
    OrderState
)

还是建成：

CREATE INDEX IDX_OrderState
ON dbo.Orders
(
    OrderState,
    OrderID
)

曾经我想当然地认为必须建成第二种方式，因为还需要对OrderID进行排序取TOP(1),但经过测试，神奇地发现两种方式的效率一样，无论“非唯一非聚集索引键”里有没有包含“聚集索引键”，都会对“非唯一非聚集索引键”+“聚集索引键”进行排序。

思考这样一个问题，假设对“非唯一非聚集索引键”，仅仅对其定义的键进行排序，如OrderState，而满足OrderState=0的可能有1亿数据，在进行数据更新的时候，首先更新聚集索引，并依次更新非聚集索引，更新索引数据首先要定位数据行才能更新，因此需要扫描这1亿数据才能找到目标行，显然这是不可接受的设计。

对于"唯一非聚集索引"来说，因为可以通过索引键便可以快速定位到索引数据行，且每个键值只会存在一行，因此失去了对“聚集索引键”进行排序的意义。

BTW, 也可以通过观察相同键值下行位置(slotid)和插入顺序来发现数据按照聚集索引键排序。

--===========================================================================

总结：

1. 对于“非唯一非聚集索引”，索引数据实际上是按照“非唯一非聚集索引键”+“聚集索引键”进行排序后存放的；

2.  对于“唯一非聚集索引”，索引数据实际上是按照“唯一非聚集索引键”进行排序后存放的；

3. 所有非聚集索引的叶子节点上都会存放RID的数据，但唯一非聚集索引的非叶子节点上不会包含RID的数据；

--===========================================================================

好好读书。。。