1890年，意大利数学家皮亚诺（Peano G）发明能填满一个正方形的曲线，叫做皮亚诺曲线。后来，由希尔伯特作出了这条曲线，又名希尔伯特曲线。Hilbert-Peano曲线是一种分形图形，它可以画得无限复杂。它的初始图元是正方形，在迭代生成的过程中，不断细化出小的正方形，图中的线段其实是用于连接各正方形的连线。它的特点是蜿蜒曲折、一气呵成，能经过平面上某一正方形区域内所有的点。希尔伯特曲线是一种奇妙的曲线，只要恰当选择函数，画出一条连续的参数曲线，当参数t在0，1区间取值时，曲线将遍历单位正方形中所有的点，得到一条充满空间的曲线。 希尔伯特曲线是一条连续而又不可导的曲线。

软件截图：

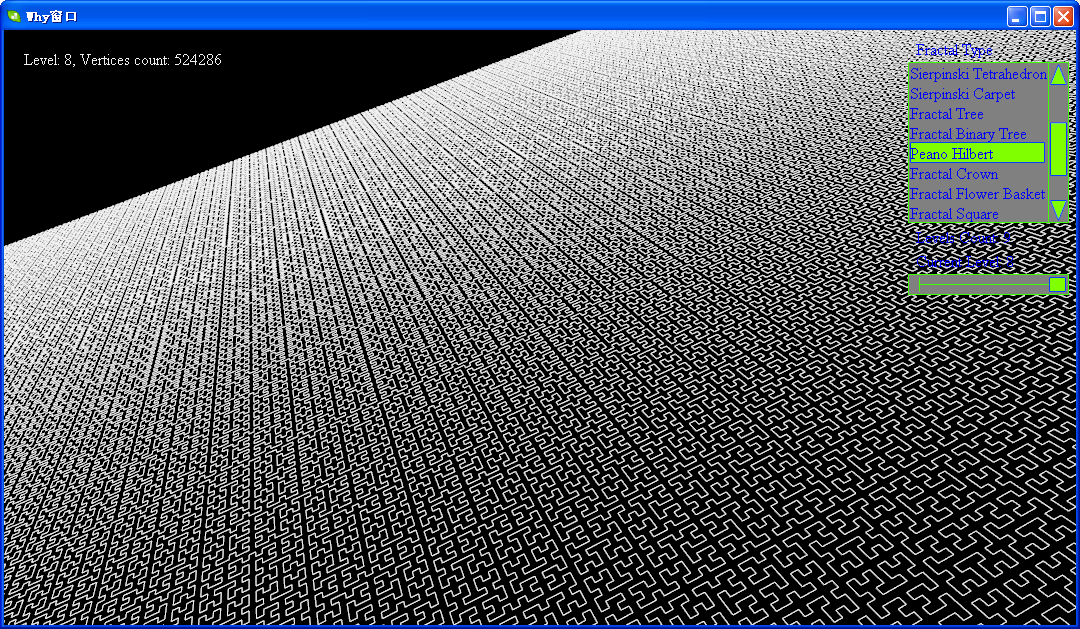
软件下载地址:http://files.cnblogs.com/WhyEngine/Fractal.7z

分形之希尔伯特－皮亚诺(Hilbert-Peano)曲线的更多相关文章

  1. 希尔伯特矩阵（Hilbert matrix）

    例: [ 1 1/2 1/3  1/2 1/3 1/4  1/3 1/4 1/5 ]   矩阵的一种,其元素A(i,j)=1/(i+j-1),i,j分别为其行标和列标. 即: [1,1/2,1/3,- ...

  2. 希尔伯特空间（Hilbert Space）是什么？

    希尔伯特空间是老希在解决无穷维线性方程组时提出的概念, 原来的线性代数理论都是基于有限维欧几里得空间的, 无法适用, 这迫使老希去思考无穷维欧几里得空间, 也就是无穷序列空间的性质. 大家知道, 在一 ...

  3. 希尔伯特空间（Hilbert Space）

    欧氏空间 → 线性空间 + 内积 ⇒ 内积空间(元素的长度,元素的夹角和正交) 内积空间 + 完备性 ⇒ 希尔伯特空间 0. 欧几里得空间 欧氏空间是一个特别的度量空间,它使得我们能够对其的拓扑性质, ...

  4. 数列极限计算中运用皮亚诺Taylor展开巧解

    这是讲义里比较精华的几个题目,今晚翻看也是想到了,总结出来(处理k/n2形式). 推广式子如下: 例题如下:

  5. 测度论--长度是怎样炼成的[zz]

    http://www.58pic.com/newpic/27882296.html http://www.58pic.com/newpic/27893137.html http://699pic.co ...

  6. KD-Tree及希尔伯特空间填充曲线的应用

    引言 我们可能会有这样的一种需求,像是打车软件中呼叫附近的车来接送自己,或者是在qq中查看附近的人.我们都需要知道距离自己一定范围内的其它目标的集合.如果将上面举例的功能抽象出来,就是要实现以某个点为 ...

  7. 18个分形图形的GIF动画演示

    这里提供18个几何线段分形的GIF动画图像.图形颜色是白色,背景色为黑色,使用最基本的黑与白以表现分形图形. (1)科赫(Koch)雪花   (2)列维(levy)曲线   (3)龙形曲线(Drago ...

  8. 高效的多维空间点索引算法 — Geohash 和 Google S2

    原文地址:https://www.jianshu.com/p/7332dcb978b2   引子 每天我们晚上加班回家,可能都会用到滴滴或者共享单车.打开 app 会看到如下的界面:     app ...

  9. Redis 高阶数据类型重温

    今天这个专题接着上一篇 Redis 的基本数据类型 继续讲解剩下的高阶数据类型:BitMap.HyperLogLog 和 GEO hash.这些数据结构的底层也都是基于我们前面说的 5 种 基本类型, ...

随机推荐

  1. Eclipse的下载及安装

    Eclipse的下载地址: https://www.eclipse.org/downloads/ 下载完成后,双击安装包即可安装 选择 Eclipse IDE for Java EE Decelope ...

  2. Carbon document

    <   Getting Started Docs Reference History Contribute Github Introduction The Carbon class is inh ...

  3. Maximum Subarray LT53

    Given an integer array nums, find the contiguous subarray (containing at least one number) which has ...

  4. 深入理解python里面类的对象的赋值

    class T(): def __init__(self): self.name= pass a=T() a.name= b=a #深入理解类,类里面的对象的赋值是指针赋值,也就是同时变的 b.nam ...

  5. java mail 读取邮件列表，

    // 准备连接服务器的会话信息 Properties props = new Properties(); props.setProperty("mail.store.protocol&quo ...

  6. 【UI测试】－－易用性

  7. maven clean package 时出现Failed to read artifact descriptor for的问题解决

    maven clean package 时出现Failed to read artifact descriptor for的问题 [ERROR] Failed to execute goal on p ...

  8. log4j日志整合输出(slf4j+commonslog+log4j+jdklogger)

    log4j日志整合输出(slf4j+commonslog+log4j+jdklogger) 博客分类: 日志   J2EE项目中,经常会用到很多第三方的开源组件和软件,这些组件都使用各自的日志组件,比 ...

  9. python入门之深浅copy

    a1=["a","b","c","aa"] b1=a1 a1[0]=" print(a1,b1) 此时结果为: ...

  10. 34、iOS App图标和启动画面尺寸

    注意:iOS所有图标的圆角效果由系统生成,给到的图标本身不能是圆角的. 1. 桌面图标 (app icon) for iPhone6 plus(@3x) : 180 x 180 for iPhone ...