python——矩阵的奇异值分解，对图像进行SVD

矩阵SVD

　　奇异值分解(Singular Value Decomposition)是一种重要的矩阵分解方法，可以看做是对方阵在任意矩阵上的推广。Singular的意思是突出的，奇特的，非凡的，按照这样的翻译似乎也可以叫做矩阵的优值分解。

　　假设矩阵A是一个m*n阶的实矩阵，则存在一个分解使得：

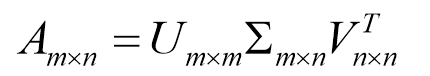
其中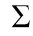，是一个对角阵，只有对角线上面有元素，对角先上面的元素称为矩阵A的奇异值，通常将其进行从大到小排列，在numpy中的api返回的是一个奇异值的向量，我们可以将其转换为对角阵。U和V都是单位正交阵，U和V的第i列是关于对应第i个特征值的奇异左右奇异向量。

　　下面给出一个实际的例子，对矩阵A进行奇异值分解：

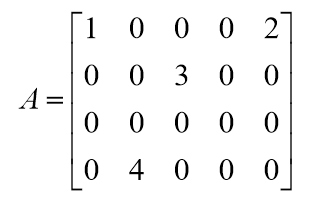
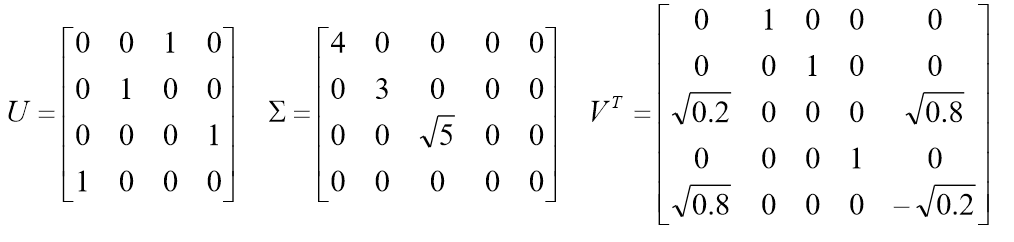
　　矩阵奇异值分解的运用非常的广泛，PCA，推荐系统，数据压缩，矩阵分解，这里就不介绍它的推导过程和原理了，想了解的同学可以查阅相关的资料，下面我们使用SVD来对图像进行分解，使用不同数量的奇异值来对图像进行压缩。我们的图像是500*980大小，总得奇异值有500个，当我们使用30个奇异值的时候，发现图像已经有点清晰了，确实很强大。

import numpy as np
import matplotlib.image as mping
import matplotlib.pyplot as plt
import matplotlib as mpl
 
def image_svd(n, pic):
    a, b, c = np.linalg.svd(pic)
    svd = np.zeros((a.shape[0],c.shape[1]))
    for i in range(0, n):
        svd[i, i] = b[i]
    img = np.matmul(a, svd)
    img = np.matmul(img, c)
    img[ img >= 255] = 255
    img[  0 >= img ] = 0
    img = img.astype(np.uint8)
    return img
 
if __name__ == '__main__':
    mpl.rcParams['font.sans-serif'] = ['SimHei']
    mpl.rcParams['axes.unicode_minus'] = False
 
    path = './simplepython/ImgSVD/a.jpg'
    img = mping.imread(path)
    print(img.shape)
 
    r = img[:, :, 0]
    g = img[:, :, 1]
    b = img[:, :, 2]
    plt.figure(figsize=(50, 100))
    for i in range(1, 31):
        r_img = image_svd(i, r)
        g_img = image_svd(i, g)
        b_img = image_svd(i, b)
        pic = np.stack([r_img, g_img, b_img], axis=2)
        print(i)
        plt.subplot(5, 6, i)
        plt.title("图像的SVD分解，使用前 %d 个特征值" %(i))
        plt.axis('off')
        plt.imshow(pic)
    plt.suptitle("图像的SVD分解")
    plt.subplots_adjust()
    plt.show()

原图片：嘉文四世