POJ1988 Cube stacking(非递归)

n有N(N<=30,000)堆方块，开始每堆都是一个方块。方块编号1 – N. 有两种操作：

nM x y ： 表示把方块x所在的堆，拿起来叠放到y所在的堆上。

nC x : 问方块x下面有多少个方块。

n操作最多有 P (P<=100,000)次。对每次C操作，输出结果。

 

 

这题挺厉害的，真的不容易想 

 

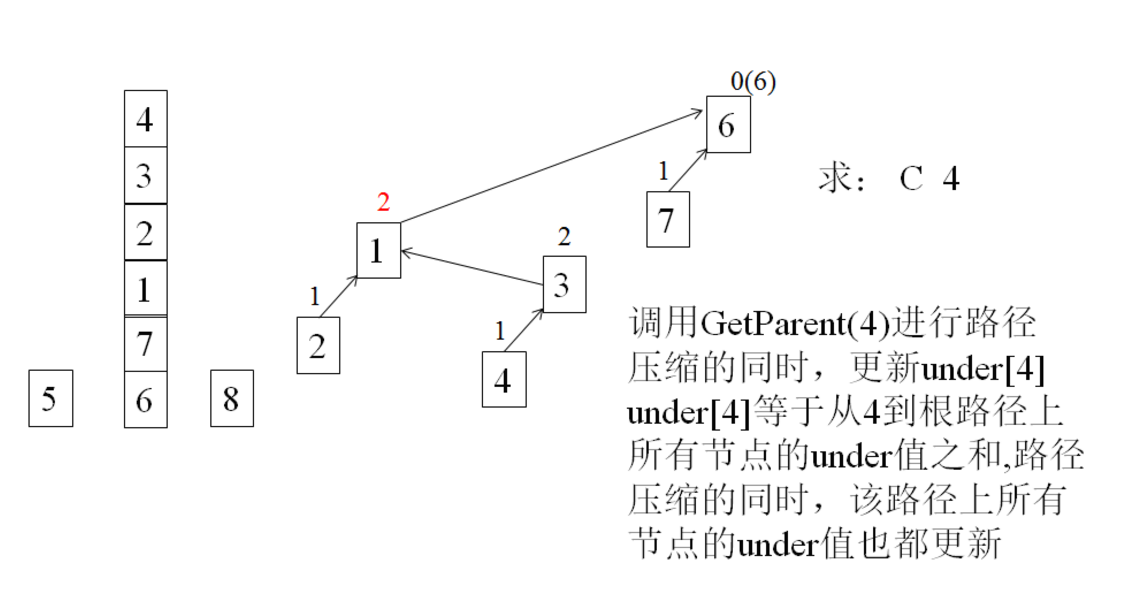
 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include<string>
 #include<algorithm>
 using namespace std;
 #define MAX 30007
 int bc[MAX],under[MAX],sum[MAX];
 void Init()
 {
     for(int i=;i<MAX;i++) {
         bc[i] = i;
         sum[i] = ;
         under[i] = ;
     }
 }

 int find(int son)
 {
     int fa = son,ans = ;

     while(bc[fa]!=fa)
     {
         ans += under[fa];
         fa = bc[fa];
     }
     //return fa;
     //Path Compression
     int temp = son,k,k1;
     while(bc[temp]!=fa)
     {
         k = bc[temp];
         bc[temp] = fa;
         k1 = under[temp];
         under[temp] = ans;
         ans -= k1;
         temp = k;
     }
     return fa;
 }

 void merge(int a,int b)
 {
     if(a == b) return ;
     a = find(a);
     b = find(b);
     if(a != b){
         bc[a] = b;
     }
     under[a] = sum[b];
     sum[b] += sum[a];
 }

 int main(int argc, char const *argv[]) {
     int p;
     while(scanf("%d",&p)!=EOF)
     {
         Init();
         char s[];
         int x,y,c;
         while(p--)
         {
             scanf("%s",s);
             if(s[] == 'M'){
                 scanf("%d%d",&x,&y);
                 merge(x,y);
             }
             else{
                 scanf("%d",&c);
                 find(c);
                 printf("%d\n",under[c]);
             }
         }
     }
     return ;
 }