Wolsey "强整数规划“ 建模的+Leapms实践——无产能批量问题

《整数规划》[1]一书作者L. A. Wolsey对批量问题（Lot-sizing Problem)做了不少“强”整数规划建模[2-5]，不是management science就是operations research，大师呀。

一个“弱”整数规划模型可以通过添加约束使之变“强” (Strong)。由于所添加的约束是线性不等式约束，就是空间上的平面并且把空间分成两半，一半留在可行解空间里，一半排除出可行解空间，于是这种约束就被叫成“割平面”(cutting plane)。

本帖记录用+Leapms对模型强化过程的实践，几乎是一个可以跟随的教程贴。如果没有+Leapms在手上，用其他建模语言和求解器也一样可以做，不过就是麻烦些。

本帖是本博客原创，本博客不转贴他人贴（除非今后说明）。

无产能批量问题（Uncapacited Lot-sizing Problem)

考虑在未来T个周期的生产-存贮问题，t (t=1,...,T) 周期的产品需求为d[t], 单位生产费用为p[t], 单位存贮费用为h[t], 生产的固定性费用为 f[t]。 要求制定生产t周期的生产量 x[t]，使得总费用最少。

这里的矛盾是：如果生产过于频繁，则要付出更多的固定性费用；如果一次生产过多，则需要付出更多存贮费，且各个周期的生产费用是不同的，应该尽量避免在高生产费用的周期生产。

各个符号有英文涵义：d[t] -- demand at time t; p[t] -- production cost at time t; h[t] -- holding cost at time t; f[t] - fixed cost at time t。

假设产能是无限的，即x[t]可以取到所有d[t]的和，因此叫做无产能批量问题。

这个例子在Wolsey书的223-227页。

设$s_t$是t时间的库存，Wolse 是这样描述模型的：

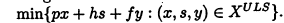
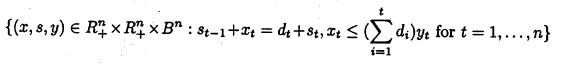
上面的第一行是说要极小化总费用；第二行是约束。熟悉+Leapms的同学知道上面的$x_t$就是x[t]了。

上面的第二行包括两个约束式，第一个是说阶段t-1的库存加上t阶段的生产等于t阶段的需求加上t阶段的库存，显然符合逻辑。就是这个：

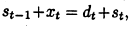
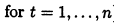
第二个是说如果在t时间内生产，则0-1变量$y_t$必须是1。这个$y_t$表示t阶段是否有生产，它要在目标里面乘上$f$, 即$fy$。

对这样的描述写成+Leapms只需要一分钟。但是写之前最好能弄些d,p,h,f的数据，否则是无本之木，没法实践。还好Wolsey给出了数据，在224页第五段：

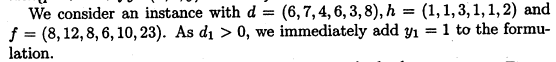
但是，Wolsey忘记给 p[t]了！发邮件给他被退回，好像老先生已经退休了。似乎实践要泡汤了。

不过思考一下没事的，因为p在研究强模型时候并不重要，只不过我们没法精准复现Wolsey的数据了，但是只要能复现模型由弱变强的性质就好。

首先我们要把“弱”模型写出来，就是这个：

min sum{t=,...,T}(h[t]s[t]+f[t]y[t])

subject to

    s[t-]+x[t]=d[t]+s[t] | t=,...,T

    x[t]<=M*y[t]|t=,...,T

    s[]=

where

    T,M are numbers

    d,h,f are sets

    s[t] is a variable of nonnegative number|t=,...,T

    x[t] is a variable of nonnegative number|t=,...,T

    y[t] is a variable of binary|t=,...,T

data_relation

    M=sum{t=,...,T}d[t]

data

    T= //阶段数

    d={     }//需求

    h={     }//单位存贮费用

    f={     } //时间t内的生产固定费用

用+Leapms松弛求解一下：

+Leapms>solve

The LP is solved to optimal.

找到线性规划最优解.非零变量值和最优目标值如下：

    .........

    x1*=

    x2*=

    x3*=

    x4*=

    x5*=

    x6*=

    y1*=0.176471

    y2*=0.205882

    y3*=0.117647

    y4*=0.176471

    y5*=0.0882353

    y6*=0.235294

    .........

    Objective*=12.1765

    .........

+Leapms>

6个y[t]都不是整数，大体跟Wolsey的图示一致：

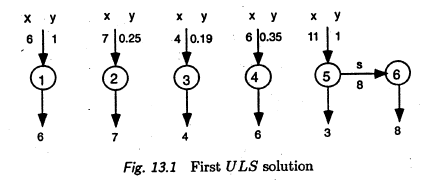
加割平面让模型变强(Strong)

加第1个割平面，原文这样写

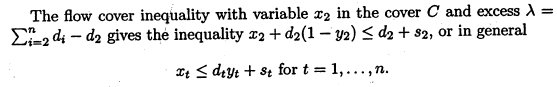
加进来的+Leapms这样写：

x[t]<=d[t]y[t]+s[t]|t=1,...,T  //割平面1

加第2个割平面，原文这样写

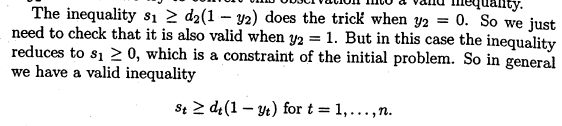
照抄写成+Leapms:

s[t]>=d[t](-y[t])|t=,...,T //割平面2

用+Leapms求解怪怪的！分析。。。分析。。。分析。。。

原来Wolsey写错了，正确的应该是：

重新写成+Leapms：

s[t-]>=d[t](-y[t])|t=,...,T //割2

加了上面两个割平面，用+Leapms松弛求解一下看：

+Leapms>solve

The LP is solved to optimal.

找到线性规划最优解.非零变量值和最优目标值如下：

    .........

    s1*=5.96296

    s2*=

    s4*=2.22581

    s5*=

    x1*=11.963

    x2*=5.03704

    x4*=8.22581

    x5*=8.77419

    y1*=

    y2*=0.148148

    y4*=

    y5*=0.258065

    .........

    Objective*=38.5472

    .........

+Leapms>

可以看见，只剩下两个0-1变量 y2和y5不是整数了。看一下Wolsey的结果：

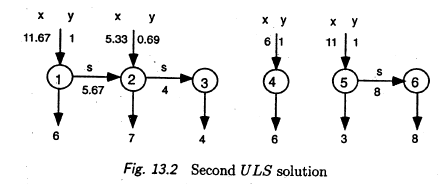
分析。。。分析。。。分析， 大体一致！

下面Wolsey还有另外两个割，他们看起来差不多，仔细看还是大不一样啊：

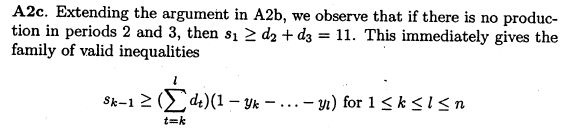
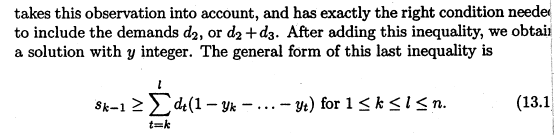
什么？这样的割也能写成+Leapms吗？

必须的！写出来是这样的：

    s[k-]>=(sum{t=k,...,l}d[t])(-sum{i=k,...,l}y[i]) | k=,...,T;l=,...,T;k<=l//割平面3

    s[k-]>=sum{t=k,...,l}(d[t](-sum{i=k,...,l}y[i])) | k=,...,T;l=,...,T;k<=l//割平面4

所有割都加完了，用+Leapms求解其松弛求一下吧：

+Leapms>solve

The LP is solved to optimal.

找到线性规划最优解.非零变量值和最优目标值如下：

    .........

    s1*=6.30249

    s2*=2.69039

    s5*=

    x1*=12.3025

    x2*=3.3879

    x3*=1.30961

    x4*=

    x5*=

    y1*=

    y2*=0.0996441

    y3*=0.327402

    y4*=

    y5*=

    .........

    Objective*=44.8078

    .........

+Leapms>

模型确实强了不少，而且与Wolsey画出的结果大体一致：

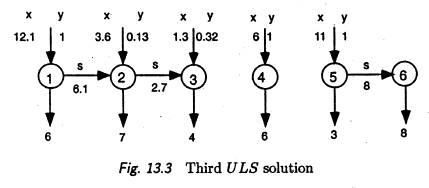
好了，实践做完了。

强模型PDF摘录

所谓强模型pdf摘录就是+Leapms自动附加生成的一个pdf文档，包含了+Leapms格式的模型和数学概念模型：

其他

问：+Leapms只能求松弛解吗？

答：当然不是。用solve命令得出的是松弛解，用mip呼叫+Leapms自身求解器得出的是整数解，用cplex命令则呼叫cplex生成整数解，用grb命令。。。。

问：上面PDF中的数学公式是+Leapms自动生成的吗？

答：当然是。

问：+Leapms能生成MPS模型吗？

答：当然能，用savemps命令就行。

问：+Leapms能生成lp格式模型吗？

答：当然能，用savelp命令就行。

问：那么能否让+Leapms生成其他建模语言模型？

答：当然能，很神奇。

附录1：+Leapms生成的lp模型

\==================================\

\Problem UncapacitatedLotSizingStrong

\.lp file gnerated by +Leapms

\==================================\

Minimize

 Obj: s1+s2+3s3+s4+s5+2s6+8y1+12y2+8y3+6y4+10y5+23y6

Subject to

 C1: s0-s1+x1=6

 C2: s1-s2+x2=7

 C3: s2-s3+x3=4

 C4: s3-s4+x4=6

 C5: s4-s5+x5=3

 C6: s5-s6+x6=8

 C7: x1-34y1<=-0

 C8: x2-34y2<=-0

 C9: x3-34y3<=-0

 C10: x4-34y4<=-0

 C11: x5-34y5<=-0

 C12: x6-34y6<=-0

 C13: s0=-0

 C14: -s1+x1-6y1<=-0

 C15: -s2+x2-7y2<=-0

 C16: -s3+x3-4y3<=-0

 C17: -s4+x4-6y4<=-0

 C18: -s5+x5-3y5<=-0

 C19: -s6+x6-8y6<=-0

 C20: s0+6y1>=6

 C21: s1+7y2>=7

 C22: s2+4y3>=4

 C23: s3+6y4>=6

 C24: s4+3y5>=3

 C25: s5+8y6>=8

 C26: s0+6y1>=6

 C27: s0+13y1+13y2>=13

 C28: s0+17y1+17y2+17y3>=17

 C29: s0+23y1+23y2+23y3+23y4>=23

 C30: s0+26y1+26y2+26y3+26y4+26y5>=26

 C31: s0+34y1+34y2+34y3+34y4+34y5+34y6>=34

 C32: s1+7y2>=7

 C33: s1+11y2+11y3>=11

 C34: s1+17y2+17y3+17y4>=17

 C35: s1+20y2+20y3+20y4+20y5>=20

 C36: s1+28y2+28y3+28y4+28y5+28y6>=28

 C37: s2+4y3>=4

 C38: s2+10y3+10y4>=10

 C39: s2+13y3+13y4+13y5>=13

 C40: s2+21y3+21y4+21y5+21y6>=21

 C41: s3+6y4>=6

 C42: s3+9y4+9y5>=9

 C43: s3+17y4+17y5+17y6>=17

 C44: s4+3y5>=3

 C45: s4+11y5+11y6>=11

 C46: s5+8y6>=8

 C47: s0+6y1>=6

 C48: s0+13y1+13y2>=13

 C49: s0+17y1+17y2+17y3>=17

 C50: s0+23y1+23y2+23y3+23y4>=23

 C51: s0+26y1+26y2+26y3+26y4+26y5>=26

 C52: s0+34y1+34y2+34y3+34y4+34y5+34y6>=34

 C53: s1+7y2>=7

 C54: s1+11y2+11y3>=11

 C55: s1+17y2+17y3+17y4>=17

 C56: s1+20y2+20y3+20y4+20y5>=20

 C57: s1+28y2+28y3+28y4+28y5+28y6>=28

 C58: s2+4y3>=4

 C59: s2+10y3+10y4>=10

 C60: s2+13y3+13y4+13y5>=13

 C61: s2+21y3+21y4+21y5+21y6>=21

 C62: s3+6y4>=6

 C63: s3+9y4+9y5>=9

 C64: s3+17y4+17y5+17y6>=17

 C65: s4+3y5>=3

 C66: s4+11y5+11y6>=11

 C67: s5+8y6>=8

Binaries

  y1

  y2

  y3

  y4

  y5

  y6

End

\==================================\

　　

附录2 MPS模型

MPS是机器交换模型，不是给人看的。供参考。

*MPS FILE GENERATED FROM +LEAPMS

NAME          UncapacitatedLotSizingStrong

ROWS

 N   OBJCT

 E   C1

 E   C2

 E   C3

 E   C4

 E   C5

 E   C6

 L   C7

 L   C8

 L   C9

 L   C10

 L   C11

 L   C12

 E   C13

 L   C14

 L   C15

 L   C16

 L   C17

 L   C18

 L   C19

 G   C20

 G   C21

 G   C22

 G   C23

 G   C24

 G   C25

 G   C26

 G   C27

 G   C28

 G   C29

 G   C30

 G   C31

 G   C32

 G   C33

 G   C34

 G   C35

 G   C36

 G   C37

 G   C38

 G   C39

 G   C40

 G   C41

 G   C42

 G   C43

 G   C44

 G   C45

 G   C46

 G   C47

 G   C48

 G   C49

 G   C50

 G   C51

 G   C52

 G   C53

 G   C54

 G   C55

 G   C56

 G   C57

 G   C58

 G   C59

 G   C60

 G   C61

 G   C62

 G   C63

 G   C64

 G   C65

 G   C66

 G   C67

COLUMNS

    s0        OBJCT           0.0000   C1              1.0000

    s0        C13             1.0000   C20             1.0000

    s0        C26             1.0000   C27             1.0000

    s0        C28             1.0000   C29             1.0000

    s0        C30             1.0000   C31             1.0000

    s0        C47             1.0000   C48             1.0000

    s0        C49             1.0000   C50             1.0000

    s0        C51             1.0000   C52             1.0000

    s1        OBJCT           1.0000   C1             -1.0000

    s1        C2              1.0000   C14            -1.0000

    s1        C21             1.0000   C32             1.0000

    s1        C33             1.0000   C34             1.0000

    s1        C35             1.0000   C36             1.0000

    s1        C53             1.0000   C54             1.0000

    s1        C55             1.0000   C56             1.0000

    s1        C57             1.0000

    s2        OBJCT           1.0000   C2             -1.0000

    s2        C3              1.0000   C15            -1.0000

    s2        C22             1.0000   C37             1.0000

    s2        C38             1.0000   C39             1.0000

    s2        C40             1.0000   C58             1.0000

    s2        C59             1.0000   C60             1.0000

    s2        C61             1.0000

    s3        OBJCT           3.0000   C3             -1.0000

    s3        C4              1.0000   C16            -1.0000

    s3        C23             1.0000   C41             1.0000

    s3        C42             1.0000   C43             1.0000

    s3        C62             1.0000   C63             1.0000

    s3        C64             1.0000

    s4        OBJCT           1.0000   C4             -1.0000

    s4        C5              1.0000   C17            -1.0000

    s4        C24             1.0000   C44             1.0000

    s4        C45             1.0000   C65             1.0000

    s4        C66             1.0000

    s5        OBJCT           1.0000   C5             -1.0000

    s5        C6              1.0000   C18            -1.0000

    s5        C25             1.0000   C46             1.0000

    s5        C67             1.0000

    s6        OBJCT           2.0000   C6             -1.0000

    s6        C19            -1.0000

    x1        OBJCT           0.0000   C1              1.0000

    x1        C7              1.0000   C14             1.0000

    x2        OBJCT           0.0000   C2              1.0000

    x2        C8              1.0000   C15             1.0000

    x3        OBJCT           0.0000   C3              1.0000

    x3        C9              1.0000   C16             1.0000

    x4        OBJCT           0.0000   C4              1.0000

    x4        C10             1.0000   C17             1.0000

    x5        OBJCT           0.0000   C5              1.0000

    x5        C11             1.0000   C18             1.0000

    x6        OBJCT           0.0000   C6              1.0000

    x6        C12             1.0000   C19             1.0000

    MARK0001  'MARKER'                 'INTORG'

    y1        OBJCT           8.0000   C7            -34.0000

    y1        C14            -6.0000   C20             6.0000

    y1        C26             6.0000   C27            13.0000

    y1        C28            17.0000   C29            23.0000

    y1        C30            26.0000   C31            34.0000

    y1        C47             6.0000   C48            13.0000

    y1        C49            17.0000   C50            23.0000

    y1        C51            26.0000   C52            34.0000

    y2        OBJCT          12.0000   C8            -34.0000

    y2        C15            -7.0000   C21             7.0000

    y2        C27            13.0000   C28            17.0000

    y2        C29            23.0000   C30            26.0000

    y2        C31            34.0000   C32             7.0000

    y2        C33            11.0000   C34            17.0000

    y2        C35            20.0000   C36            28.0000

    y2        C48            13.0000   C49            17.0000

    y2        C50            23.0000   C51            26.0000

    y2        C52            34.0000   C53             7.0000

    y2        C54            11.0000   C55            17.0000

    y2        C56            20.0000   C57            28.0000

    y3        OBJCT           8.0000   C9            -34.0000

    y3        C16            -4.0000   C22             4.0000

    y3        C28            17.0000   C29            23.0000

    y3        C30            26.0000   C31            34.0000

    y3        C33            11.0000   C34            17.0000

    y3        C35            20.0000   C36            28.0000

    y3        C37             4.0000   C38            10.0000

    y3        C39            13.0000   C40            21.0000

    y3        C49            17.0000   C50            23.0000

    y3        C51            26.0000   C52            34.0000

    y3        C54            11.0000   C55            17.0000

    y3        C56            20.0000   C57            28.0000

    y3        C58             4.0000   C59            10.0000

    y3        C60            13.0000   C61            21.0000

    y4        OBJCT           6.0000   C10           -34.0000

    y4        C17            -6.0000   C23             6.0000

    y4        C29            23.0000   C30            26.0000

    y4        C31            34.0000   C34            17.0000

    y4        C35            20.0000   C36            28.0000

    y4        C38            10.0000   C39            13.0000

    y4        C40            21.0000   C41             6.0000

    y4        C42             9.0000   C43            17.0000

    y4        C50            23.0000   C51            26.0000

    y4        C52            34.0000   C55            17.0000

    y4        C56            20.0000   C57            28.0000

    y4        C59            10.0000   C60            13.0000

    y4        C61            21.0000   C62             6.0000

    y4        C63             9.0000   C64            17.0000

    y5        OBJCT          10.0000   C11           -34.0000

    y5        C18            -3.0000   C24             3.0000

    y5        C30            26.0000   C31            34.0000

    y5        C35            20.0000   C36            28.0000

    y5        C39            13.0000   C40            21.0000

    y5        C42             9.0000   C43            17.0000

    y5        C44             3.0000   C45            11.0000

    y5        C51            26.0000   C52            34.0000

    y5        C56            20.0000   C57            28.0000

    y5        C60            13.0000   C61            21.0000

    y5        C63             9.0000   C64            17.0000

    y5        C65             3.0000   C66            11.0000

    y6        OBJCT          23.0000   C12           -34.0000

    y6        C19            -8.0000   C25             8.0000

    y6        C31            34.0000   C36            28.0000

    y6        C40            21.0000   C43            17.0000

    y6        C45            11.0000   C46             8.0000

    y6        C52            34.0000   C57            28.0000

    y6        C61            21.0000   C64            17.0000

    y6        C66            11.0000   C67             8.0000

RHS

    RHS1      C1              6.0000   C2              7.0000

    RHS1      C3              4.0000   C4              6.0000

    RHS1      C5              3.0000   C6              8.0000

    RHS1      C20             6.0000   C21             7.0000

    RHS1      C22             4.0000   C23             6.0000

    RHS1      C24             3.0000   C25             8.0000

    RHS1      C26             6.0000   C27            13.0000

    RHS1      C28            17.0000   C29            23.0000

    RHS1      C30            26.0000   C31            34.0000

    RHS1      C32             7.0000   C33            11.0000

    RHS1      C34            17.0000   C35            20.0000

    RHS1      C36            28.0000   C37             4.0000

    RHS1      C38            10.0000   C39            13.0000

    RHS1      C40            21.0000   C41             6.0000

    RHS1      C42             9.0000   C43            17.0000

    RHS1      C44             3.0000   C45            11.0000

    RHS1      C46             8.0000   C47             6.0000

    RHS1      C48            13.0000   C49            17.0000

    RHS1      C50            23.0000   C51            26.0000

    RHS1      C52            34.0000   C53             7.0000

    RHS1      C54            11.0000   C55            17.0000

    RHS1      C56            20.0000   C57            28.0000

    RHS1      C58             4.0000   C59            10.0000

    RHS1      C60            13.0000   C61            21.0000

    RHS1      C62             6.0000   C63             9.0000

    RHS1      C64            17.0000   C65             3.0000

    RHS1      C66            11.0000   C67             8.0000

BOUNDS

 FR BND       s0

 FR BND       s1

 FR BND       s2

 FR BND       s3

 FR BND       s4

 FR BND       s5

 FR BND       s6

 FR BND       x1

 FR BND       x2

 FR BND       x3

 FR BND       x4

 FR BND       x5

 FR BND       x6

 UP BND       y1

 UP BND       y2

 UP BND       y3

 UP BND       y4

 UP BND       y5

 UP BND       y6         

ENDATA

附录3 整数规划解

+Leapms>mip

relexed_solution=44.8078; number_of_nodes_branched=; memindex=(,)

The Problem is solved to optimal as an MIP.

找到整数规划的最优解.非零变量值和最优目标值如下：

  .........

    s1* =

    s2* =

    s5* =

    x1* =

    x4* =

    x5* =

    y1* =

    y4* =

    y5* =

  .........

    Objective*=

  .........

+Leapms>

参考文献

[1] Wolsey L A. Integer Programming. New York: Jonh Wiley & Sons, 1998 / ISBN 978-0-471-28366-9

[2] Barany I. Strong Formulations for Multi-Item Capacitated Lot Sizing[J]. Management Science, 1984, 30(30):1255-1261.

[3] Wolsey L A. Uncapacitated Lot-Sizing Problems with Start-Up Costs[J]. Operations Research, 1989, 37(5):741-747.

[4] Belvaux G, Wolsey L A. bc-prod: A Specialized Branch-and-Cut System for Lot-Sizing Problems[J]. Management Science, 2000, 46(5):724-738.

[5] Wolsey L A. Erratum: A tight formulation for uncapacitated lot-sizing with stock upper bounds[J]. Mathematical Programming, 2017, 161(1-2):1-7.

Wolsey "强整数规划“ 建模的+Leapms实践——无产能批量问题的更多相关文章

  1. Wolsey“强整数规划模型”经典案例之一单源固定费用网络流问题

    Wolsey“强整数规划模型”经典案例之一单源固定费用网络流问题 阅读本文可以理解什么是“强”整数规划模型. 单源固定费用网络流问题见文献[1]第13.4.1节(p229-231),是"强整 ...

  2. 流水车间调度算法分析的简单+Leapms实践--混合整数规划的启发式建模

    流水车间调度算法分析的简单+Leapms实践--混合整数规划的启发式建模 清华大学出版社出版的白丹宇教授著作<流水车间与开放车间调度算法渐近分析>采用渐近分析方法分析多个NP-难类启发调度 ...

  3. 【翻译】ScyllaDB数据建模的最佳实践

    文章翻译自Scylla官方文档:https://www.scylladb.com/2019/08/20/best-practices-for-data-modeling/ 转载请注明出处:https: ...

  4. 技术分享丨数据仓库的建模与ETL实践技巧

    摘要:如何搭建数据仓库,在这个过程中都应该遵循哪些方法和原则,项目实践中有哪些技巧. 一.数据仓库的“心脏” 首先来谈谈数据模型.模型是现实世界特征的模拟和抽象,比如地图.建筑设计沙盘,飞机模型等等. ...

  5. 数据仓库建模与ETL实践技巧

    数据分析系统的总体架构分为四个部分 —— 源系统.数据仓库.多维数据库.客户端(图一:pic1.bmp) 其中,数据仓库(DW)起到了数据大集中的作用.通过数据抽取,把数据从源系统源源不断地抽取出来, ...

  6. 学习懈怠的时候，可以运行Qt自带的Demo，或者Delphi控件自带的Demo，或者Cantu书带的源码，运行一下Boost的例子（搞C++不学习Boost/Poco/Folly绝对是一大损失，有需要使用库要第一时间想到）（在六大的痛苦经历说明，我的理论性确实不强，更适合做实践）

    这样学还不用动脑子,而且熟悉控件也需要时间,而且慢慢就找到感觉了,就可以精神抖擞的恢复斗志干活了.或者Cantu书带的源码. 并且可以使用Mac SSD运行Qt的Demo,这样运行速度快一点. 此外, ...

  7. 【实践】jdbc批量插入数据

    参考文献:http://my.oschina.net/u/1452675/blog/203670 http://superjavason.iteye.com/blog/255423 /*测试批量写入数 ...

  8. Mysql数据库实践操作之————批量插入数据（100万级别的数据）

    第一种方法:使用insert into 插入 从Redis每次获取100条数据,根据条件去插入到Mysql数据库中: 条件: 如果当前队列中的值大于1000条,则会自动的条用该方法,该方法每次获取从队 ...

  9. 【DDD】领域驱动设计实践 —— 业务建模实例（‘发布帖子’）

    本文是基于上一篇‘业务建模小招数’的实践,后面的多篇博文类似.本文主要讲解‘发表帖子’场景的业务建模,包括:业务建模.业务模型.示例代码:示例代码会使用java编写,文末附有github地址.相比于& ...

随机推荐

  1. 「SDOI 2018」战略游戏

    题目大意: 给一个$G=(V,E)$,满足$|V|=n$,$|E|=m$,且保证图联通,有Q个询问,每组询问有s个点,求图中有多少点满足:将其删去后,这s个点中存在一对点集$(a,b)$不联通且删去点 ...

  2. BZOJ_1861_[Zjoi2006]Book 书架_splay

    BZOJ_1861_[Zjoi2006]Book 书架_splay 题意: 小T有一个很大的书柜.这个书柜的构造有些独特,即书柜里的书是从上至下堆放成一列.她用1到n的正整数给每本书都编了号. 小T在 ...

  3. BZOJ4554: [Tjoi2016&Heoi2016]游戏 luoguP2825 loj2057

    题面描述:尽可能多的放置符合要求的炸弹. 分析: 在i,j处放置炸弹,则在第i行,上一个硬石头之后,下一个硬石头之前,第j列,上一个硬石头之后,下一个硬石头之前,不能再次放置炸弹. 首先,这个题,一看 ...

  4. 高数量类别特征（high-cardinality categorical attributes）的预处理方法

    high-cardinality categorical attributes,从字面上理解,即对于某个category特征,不同值的数量非常多,这里暂且把它叫做高数量类别属性.反之,即低数量类别属性 ...

  5. java基于BasicPlayer调用 播放音乐

    无聊中想想用java调用下听音乐的api.晚上很多文章用的比较老大方法了,都是用原生的代码写,而且不支持mp3格式,BasicPlayer第三方包提供了很好的api调用,简单的3行代码就可以调用mp3 ...

  6. MYSQL——数据库存储引擎！

    本人安装mysql版本为:mysql  Ver 14.14 Distrib 5.7.18, for Win64 (x86_64),查看mysql的版本号方式:cmd-->mysql --vers ...

  7. 关于分布式锁原理的一些学习与思考-redis分布式锁，zookeeper分布式锁

    首先分布式锁和我们平常讲到的锁原理基本一样,目的就是确保,在多个线程并发时,只有一个线程在同一刻操作这个业务或者说方法.变量. 在一个进程中,也就是一个jvm 或者说应用中,我们很容易去处理控制,在j ...

  8. PostGreSQL(1)-源码安装

    目录 简述 一.格式化磁盘 二.源码安装 PostGreSql 1. 安装 readline-devel 2. 安装 PostGresql 3. 设置环境变量 三. 初始化 1. 设置运行用户 2. ...

  9. MD5加密Util

    目录 (1)需要导入的包 (2)MD5Util类 (3)使用举例 (1)需要导入的包 <dependency> <groupId>org.apache.commons</ ...

  10. css，解决文字与图片对齐的问题

    测试代码: <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF ...