LeetCode(119):杨辉三角 II
Easy!
题目描述:
给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行。

在杨辉三角中,每个数是它左上方和右上方的数的和。
示例:
输入: 3
输出: [1,3,3,1]
进阶:
你可以优化你的算法到 O(k) 空间复杂度吗?
解题思路:
杨辉三角想必大家并不陌生,应该最早出现在初高中的数学中,其实就是二项式系数的一种写法。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
杨辉三角形第n层(顶层称第0层,第1行,第n层即第n+1行,此处n为包含0在内的自然数)正好对应于二项式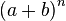 展开的系数。例如第二层1 2 1是幂指数为2的二项式
展开的系数。例如第二层1 2 1是幂指数为2的二项式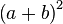 展开形式
展开形式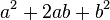 的系数。
的系数。
杨辉三角主要有下列五条性质:
- 杨辉三角以正整数构成,数字左右对称,每行由1开始逐渐变大,然后变小,回到1。
- 第
 行的数字个数为
行的数字个数为 个。
个。 - 第
 行的第
行的第 个数字为组合数
个数字为组合数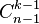 。
。 - 第
 行数字和为
行数字和为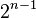 。
。 - 除每行最左侧与最右侧的数字以外,每个数字等于它的左上方与右上方两个数字之和(也就是说,第
 行第
行第 个数字等于第
个数字等于第 行的第
行的第 个数字与第
个数字与第 个数字的和)。这是因为有组合恒等式:
个数字的和)。这是因为有组合恒等式: 。可用此性质写出整个杨辉三角形。
。可用此性质写出整个杨辉三角形。
由于题目有额外限制条件,程序只能使用O(k)的额外空间,那么这样就不能把每行都算出来,而是要用其他的方法,。最先考虑用的是第三条性质,算出每个组合数来生成第n行系数,代码如下:
C++ 解法一:
/**
* NOT Correct!
*/
class Solution {
public:
vector<int> getRow(int rowIndex) {
vector<int> out;
if (rowIndex < ) return out; for (int i = ; i <= rowIndex; ++i) {
if ( i == || i == rowIndex)
out.push_back();
else
out.push_back (computeCnk(rowIndex, i));
}
return out;
} int computeCnk(int n, int k) {
if (k > n) return ;
else if (k > n/) k = n - k;
int numerator = , denomator = ;
for (int i = ; i < k; ++i) {
numerator *= n - i;
denomator *= k - i;
}
if (denomator != ) return numerator/denomator;
else return ;
}
};
本地调试输出前十行,没啥问题,拿到OJ上测试,程序在第18行跪了,中间有个系数不正确。那么问题出在哪了呢,仔细找找,原来出在计算组合数那里,由于算组合数时需要算连乘,而整形数int的数值范围只有-32768到32768之间,那么一旦n值过大,连乘肯定无法计算。而丧心病狂的OJ肯定会测试到成百上千行,所以这个方法不行。那么我们再来考虑利用第五条性质,除了第一个和最后一个数字之外,其他的数字都是上一行左右两个值之和。那么我们只需要两个for循环,除了第一个数为1之外,后面的数都是上一次循环的数值加上它前面位置的数值之和,不停地更新每一个位置的值,便可以得到第n行的数字。
C++ 解法二:
class Solution {
public:
vector<int> getRow(int rowIndex) {
vector<int> out;
if (rowIndex < ) return out;
out.assign(rowIndex + , );
for (int i = ; i <= rowIndex; ++i) {
if ( i == ) {
out[] = ;
continue;
}
for (int j = rowIndex; j >= ; --j) {
out[j] = out[j] + out[j-];
}
}
return out;
}
};
LeetCode(119):杨辉三角 II的更多相关文章
- Java实现 LeetCode 119 杨辉三角 II
119. 杨辉三角 II 给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行. 在杨辉三角中,每个数是它左上方和右上方的数的和. 示例: 输入: 3 输出: [1,3,3,1] 进阶: ...
- LeetCode(119. 杨辉三角 II)
问题描述 给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行. 在杨辉三角中,每个数是它左上方和右上方的数的和. 示例: 输入: 3 输出: [1,3,3,1] 进阶: 你可以优化你的 ...
- 【LeetCode】119. 杨辉三角 II Pascal‘s Triangle II(Python & Java)
作者: 负雪明烛 id: fuxuemingzhu 个人博客: http://fuxuemingzhu.cn/ 目录 题目描述 题目大意 解题思路 方法一: 空间复杂度 O ( k ∗ ( k + 1 ...
- 119.杨辉三角II
这道题和第118题是一样的,需要注意这道题目对行数的要求 # 定义一个列表,用来存放数据 num_list = [] for index1 in ran ...
- 力扣119. 杨辉三角 II
原题 1 class Solution: 2 def getRow(self, rowIndex: int) -> List[int]: 3 ans = [1] 4 for i in range ...
- LeetCode119.杨辉三角 II
119.杨辉三角 II 描述 给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行. 在杨辉三角中,每个数是它左上方和右上方的数的和. 示例 输入: 3 输出: [1,3,3,1] 进阶 ...
- LeetCode:杨辉三角【118】
LeetCode:杨辉三角[118] 题目描述 给定一个非负整数 numRows,生成杨辉三角的前 numRows 行. 在杨辉三角中,每个数是它左上方和右上方的数的和. 示例: 输入: 5 输出: ...
- [LeetCode] 119. Pascal's Triangle II 杨辉三角 II
Given an index k, return the kth row of the Pascal's triangle. For example, given k = 3,Return [1,3, ...
- LeetCode 118:杨辉三角 II Pascal's Triangle II
公众号:爱写bug(ID:icodebugs) 作者:爱写bug 给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行. Given a non-negative index k whe ...
随机推荐
- java.lang.NoSuchMethodError: org.apache.curator.framework.api.CreateBuilder.creatingParentsIfNeeded()Lorg/apache/curator/framework/api/ProtectACLCreateModeStatPathAndBytesable;
1 错误信息 java.lang.NoSuchMethodError: org.apache.curator.framework.api.CreateBuilder.creatingParentsIf ...
- GitHub贡献第一的公司是谁?微软开源软件列表
参考:http://www.infoq.com/cn/news/2017/03/GitHub-first-Microsoft-open-sour 提起微软公司,不少人第一反应是老牌巨头专注于私有化软件 ...
- vue学习之template标签
HTML5提供的新标签,具有以下特性: 1.该元素天生display:none,同时模板元素内部内容也是隐藏的 2.位置任意,可以在<head>中,也可以在<body>或者&l ...
- Spring基础3
一.AOP 1)AOP简介: Aspect Oriented Programming,面向切面编程 通过预编译方式和动态代理实现程序功能的一种技术,AOP是OOP的延续,是函数式编程的一种衍生范例.利 ...
- Kotlin中构造方法的参数var val 和 什么都没有的区别
1.什么都没有,在该类中使不能使用的, 这个参数的作用就是,传递给父类的构造方法 2.使用var 可以在类中使用,相当于 我们声明了一个该类中定义了一个private 的成员变量 3.val表示不让修 ...
- PTA 逆散列问题 (30 分)(贪心)
题目链接:https://pintia.cn/problem-sets/1107178288721649664/problems/1107178432099737614 题目大意: 给定长度为 N 的 ...
- Android 5.0以上Material Design 沉浸式状态栏
偶然在知乎上看到这个问题,Android 5.0 如何实现将布局的内容延伸到状态栏,之前也见过多个应用的这个功能,但是知乎上的答案却没有一个真正实现此功能的一类是把标题栏设置App主题颜色,一类是提取 ...
- k64 datasheet学习笔记45---10/100-Mbps Ethernet MAC(ENET)之功能描述
1.前言 本文是对K64 datasheet 之ENET部分的功能描述,将对每个部分进行详细说明 2.Ethernet MAC frame formats MAC帧组成格式 (1)7字节前导码:如按最 ...
- python3+selenium框架设计10-发送邮件
使用python3的email模块和smtplib模块可以实现发送邮件的动能.email模块用来生成email,smtplib模块用来发送邮件,接下来看如何在生成测试报告之后,并将报告放在邮件附件中并 ...
- Windows下return,exit和ExitProcess的区别和分析
通常,我们为了使自己的程序结束,会在主函数中使用return或调用exit().在windows下还有ExitProcess()和TerminateProcess()等函数. 本文的目的是比较以上几种 ...
