HDU1542-Atlantis【离散化&线段树&扫描线】个人认为很全面的详解

刚上大一的时候见过这种题，感觉好牛逼哇，这都能算

如今已经不打了，不过适当写写题保持思维活跃度还是不错的，又碰到这种题了，想把它弄出来

说实话，智商不够，看了很多解析，花了4、5个小时才弄明白

网上好多都是直说一半，弄得我很难受，需要查看很多题解不断对比才清楚

首先线段树这玩意，不光是线段树吧，只要牵扯到递归都很抽象，要想好久

如果中途有哪些不懂，继续看，代码我尽量做到每一行都有注释

1.离散化

先说离散化，这里面牵扯到小数，而线段树是维护一个整数区间，这是我们首先遇到的问题

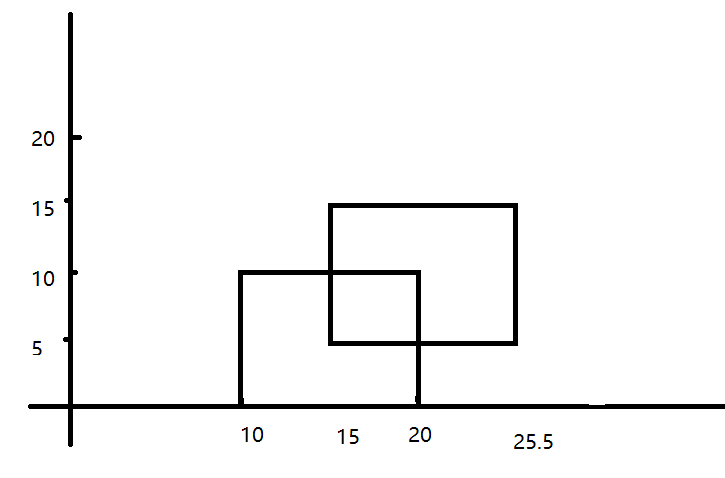
比如这种情况，第二个矩形刚好多了0.5怎么办哦

这时候就要用离散化来处理了，我个人感觉离散化说白了就是映射，先把一些难算的数值映射到一些简单的数值上算完了再换回去

比如解物理题的时候先把一些不能拆开但很复杂的表达式用符号代替，算完了再换回去

那么两个矩形四条竖边，对应的x分别是10、15、20、25.5，那么久把这个不同的x值，存到数组里dif_x[4] = {10,15,20,25.5}

用的时候，比如你要用到15~25.5这条边的时候就用dif_x[3] - dif_x[1]得到10.5，就ok了

2.扫描线

你就想象有一根水平的线从下往上走，碰到边就更新，这个有前人说的很详细，我就直接拿来用了

http://www.cnblogs.com/Konjakmoyu/p/6050343.html

这个讲的很好，我一开始理解扫描线就是看的这个

3.线段树

首先你要有线段树的基本知识嘛，这个就不说了

说一下里面值的定义

struct node2
{
    int l,r,cnt;
    double len;
}tree[];

这个也是这道题里面最难理解的一部分

线段树到底维护的什么，或者说存放的什么？

首先，根据扫描线的思路，你要存放的是当前扫描线的长度，这样才能乘高度差

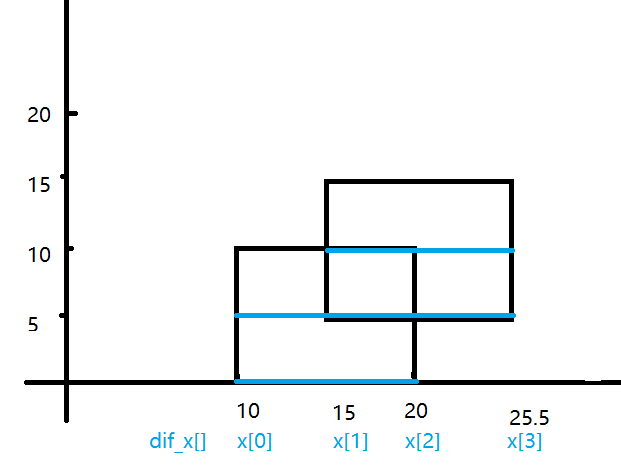
那么你每次要更新的就是蓝线的长度

那么蓝线的长度是不是可以由 dif_x[r] - dif_x[l]得到

比如我们第一次更新的这条蓝线是10~20，那么是不是可以由dif_x[] 数组的下标0~2来表示

第二次更新的蓝线是10~25.5，是不是可以由0~3来表示

最后一次由1~3表示

那我们就知道了，线段树里的l，r其实存的是该结点所能涉及的dif_x[]数组的下标

结点1的l，r分别是0,3那么就是10——25.5这条线段中，被覆盖的长度

但是这里就有一个问题了，0——1的长度可以理解，但是0是一个点，它的长度就是0啊

所以我么规定，每一个坐标表示从它到它+1的点的长度

比如tree[4]表示，0~1的长度是5

tree[6]表示，2~3的长度是5.5

cnt表示该结点是否被覆盖，参与这次面积的计算

double len 当然表示的就是该线段的长度了

补充

还需要一个比较重要的结构体

struct node
{
    double x1,x2,y;
    int flag;
    void init(double l,double r,double h,int key) {
        x1 = l; x2 = r; y = h; flag = key;
    }
}line[];

这个结构体代表每一根横线

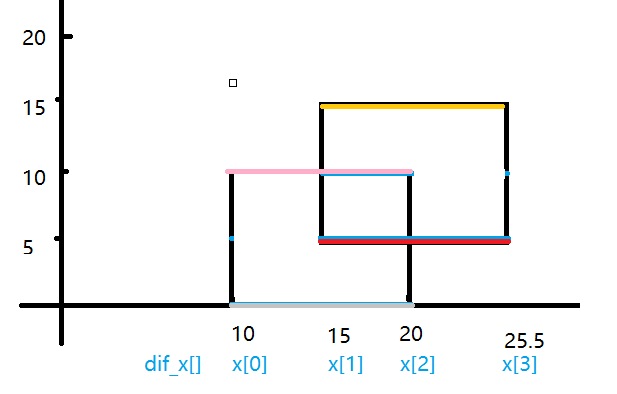
比如灰线代表line[0]，红线line[1]，粉线line[2]以此类推

x1,x2就是这根线的左右端点坐标，y是这根线的y轴坐标，flag表示这根线是矩形的下面的线还是上面的线

这个很重要，如果是下面的线，在更新tree[]的时候，由于你是从下往上扫，所以要+1

如果是上面的线，在更新线段树tree[]的时候，由于你是从下往上扫，所以要-1，表示你已经扫完了某个矩形，你要将矩形的上边减掉

要讲的就这么多了吧

看代码

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;

 double dif_x[];//记录不同的x坐标

 struct node
 {
     double x1,x2,y;
     int flag;//各个参数上面说过
     void init(double l,double r,double h,int key) {
         x1 = l; x2 = r; y = h; flag = key;
     }
 }line[];

 bool cmp(node a, node b)
 {
     return a.y < b.y;
 }

 struct node2
 {
     int l,r,cnt;//各个参数上面说过
     double len;
 }tree[];

 void build_tree(int id,int l,int r)//最基本的线段树建树不多说
 {
     tree[id].l = l;
     tree[id].r = r;
     tree[id].cnt = ;
     tree[id].len = ;
     if(l==r){
         return;
     }
     int mid = (r + l)>>;
     build_tree(id<<,l,mid);
     build_tree((id<<)+,mid+,r);
 }

 void getlen(int id)
 {
     if(tree[id].cnt >= ) { //如果该段被覆盖那么就直接由dif_x数组获得长度
         tree[id].len = dif_x[tree[id].r+] - dif_x[tree[id].l];//看了注释①以后，应该不难理解了
     }
     else {
         tree[id].len = tree[id<<].len + tree[(id<<)|].len;//如果没有被覆盖，那么应该是由左右孩子的和
     }
 }

 void update(int id,int l,int r,int v)
 {
     if(tree[id].l==l && tree[id].r==r) {//目标区间
         tree[id].cnt += v;//标记是否覆盖
         getlen(id);//算一下长度
         return;
     }
     int mid = (tree[id].l+tree[id].r)>>;
     if(r <= mid){
         update(id<<,l,r,v);//更新左子树
     }
     else if(l > mid) {
         update((id<<)+,l,r,v);//更新右子树
     }
     else {
         update(id<<,l,mid,v);
         update((id<<)+,mid+,r,v);//更新左右子树
     }
     getlen(id);//push_up一下
 }

 int mySearch(double p, int l, int r)//二分找p在dif_x数组中的下标
 {
     while(l <= r)
     {
         int mid = (l + r)>>;
         if(dif_x[mid] == p){
             return mid;//返回这个下标
         }
         if(dif_x[mid] < p) {
             l = mid + ;
         }
         else {
             r = mid - ;
         }
     }
 }

 int main()
 {
     int n,noc = ;//number_of_case
     while(~scanf("%d",&n))//输入
     {
         if (n == ) break;
         noc ++;
         double x1,y1,x2,y2;//矩形的位置参数
         int line_num = ;//一共有多少条横线
         for(int i=;i<n;i++)//输入
         {
             scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
             line[line_num].init(x1,x2,y1,);//下面的线，flag = 1
             dif_x[line_num++] = x1;//数据中一共有多少个不同的横坐标
             line[line_num].init(x1,x2,y2,-);//上面的线，flag = -1
             dif_x[line_num++] = x2;
         }
         sort(line, line+line_num, cmp);//对横线由低到高进行排序，因为你是从下往上扫描的
         sort(dif_x, dif_x+line_num);//对dif_x去重，要先排个序，这样更方便
         int dif_x_num = unique(dif_x, dif_x+line_num) - dif_x;//dif_x_num表示去重后不同的x坐标的数量
         build_tree(,,dif_x_num-);//建立线段树
         double ans = ;//最终的答案
         for(int i=;i<line_num-;i++)//开始扫描
         {
             int line_l = mySearch(line[i].x1,,dif_x_num-);//第i根线的左端点对应在dif_x的下标
             int line_r = mySearch(line[i].x2,,dif_x_num-)-;//右边要减一，看注释①
             update(,line_l,line_r,line[i].flag);//更新线段树
             ans += tree[].len * (line[i+].y - line[i].y);//求面积，tree[1]就是总长度嘛
         }
         printf("Test case #%d\n",noc);
         printf("Total explored area: %.2lf\n\n",ans);
     }
 }

注释① 这里我看了n多题解，没一个说为什么-1，管这个我就懵逼了70%的时间，希望看了这个会节约你很多时间
其实我前面已经说了，每个点代表从它到它+1的点的长度，那么你要求0~3的长度，其实要求的是0~2的长度

好辛苦，终于写完了，希望对你有帮助！