图论分支-Tarjan初步-点双连通分量

上一次我们讲到了边双，这次我们来看点双。

说实话来说，点双比边双稍微复杂一些；

学完边双，我们先看一道题

第一问都不用说了吧，多余的道路，明显的割边。

是不是首先想到用边双，但是我们来看一个图：

有点丑，但是凑活看吧。

它是一个边双，但是！！！！它竟然没有冲突的边！！！

此时我们就要用点双了（是不是想打死我，竟然没讲，先坑人）

先看概念

都说概念是非常重要的，但是概念似乎有点笼统，可以附图解说

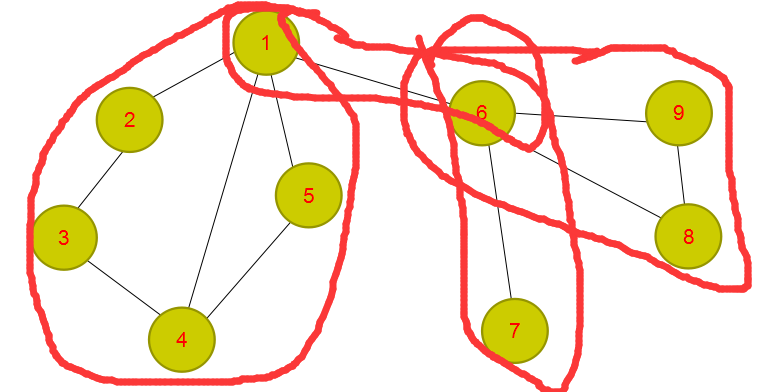
点双的一大特点是它可以重复用点，而那个点就是割点，而我们的缩点操作也是用割点连接各个点双的。

那么我们来看算法，我们在Tarjan时，用栈去维护点双，之后用vector去储存。

我们直接来看上面的题，就会明白这不是点双吗？

然后寻找规律，我们会发现，每一个点双中，只要边个数大于点个数，那么这里的边都是冲突的，那么我们的Code就跃然纸上了

#include<bits/stdc++.h>
#define maxn 10007
#define M 100007
using namespace std;
int n,m,cent=,t,head[maxn],low[maxn],dfn[maxn],ans1,ans2;
int stackk[maxn],cnt,top,root,cut[maxn],col[maxn],vis[maxn];
int ol;
vector<int >dcc[maxn];
struct node{
    int next,to;
}edge[M*];
 
inline void add(int u,int v){
    edge[++cent]=(node){head[u],v};head[u]=cent;
}
 
void Tarjan(int x,int fa){
    dfn[x]=low[x]=++t;
    stackk[++top]=x;//入栈
    if(x==root&&head[x]==){//不联通时的孤立点
        dcc[++cnt].push_back(x);
        return ;
    }
    for(int i=head[x];i;i=edge[i].next){
        int y=edge[i].to;
        if(!dfn[y]){
            Tarjan(y,i);
            low[x]=min(low[x],low[y]);//与其他的一样
            if(low[y]>=dfn[x]){
                if(low[y]>dfn[x]) ans1++;//记录割边个数
                int z;cnt++;
                do{
                    z=stackk[top--];//从栈中取出
                    dcc[cnt].push_back(z);//存入
                }while(z!=y);//停止条件，这个可以想一想为什么
                dcc[cnt].push_back(x);//把割点也存进去
            }
        }else if((i^)!=fa) low[x]=min(low[x],dfn[y]);
    }
}
 
void clear(){
    ans1=ans2=top=cnt=t=ol=;cent=;
    memset(head,,sizeof head);
    memset(low,,sizeof low);
    memset(dfn,,sizeof dfn);
    memset(stackk,,sizeof stackk);
    memset(dcc,,sizeof dcc);
    memset(col,,sizeof col);
    memset(edge,,sizeof edge);
}
 
int main(){
//    freopen("way.in","r",stdin);
//    freopen("way.out","w",stdout);
    while(scanf("%d%d",&n,&m)){
        if(n==&&m==)break;
        clear();
        int a,b;
        for(int i=;i<=m;i++){
            scanf("%d%d",&a,&b);
            add(a+,b+),add(b+,a+);//由于点从零开始，那么我们+1即可
        }
        for(int i=;i<=n;i++){
            if(!dfn[i]) root=i,Tarjan(i,-);
        }
        for(int i=;i<=cnt;i++,ol=){
            for(int j=;j<dcc[i].size();j++){
                vis[dcc[i][j]]=;//记录点双上的点
            }
            for(int k=;k<dcc[i].size();k++){
                for(int j=head[dcc[i][k]];j;j=edge[j].next){
                    if(vis[edge[j].to]) ol++;//ol统计边数
                }
            }
            if(ol/>dcc[i].size()) ans2+=ol/;//由于是双向边，ol会统计量词
            memset(vis,,sizeof(vis));
        }
        printf("%d %d\n",ans1,ans2);
    }
}

那么我们就应该懂了一些基本的概念，和简单的操作，那么，留一个彩蛋，我们该如何去缩点连接呢？