Andrew Ng-ML-第八章-正则化

1.过度拟合overfitting

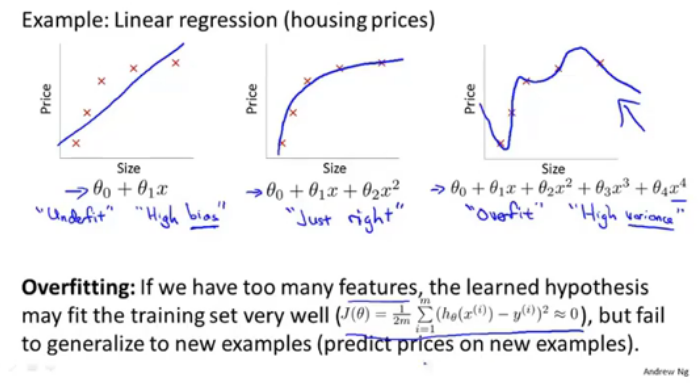
过度拟合，因为有太多的特征+过少的训练数据，学习到的假设可能很适应训练集，但是不能泛化到新的样例。即泛化generalize能力差。

解决办法：

1.手动/使用选择算法来确定保留的特征。

2.当所有的特征都对结果有一定贡献时，需要正则化，保留所有特征，但是降低θ的量级或者值。

2.正则化

在代价函数中加入惩罚项（正则化项），即对所有系数平方求和，乘上惩罚系数，这样就会降低各系数的量级，从而使分类模型形式更加简单，更简单的意思在这里可以理解为，像是预测房价的，如果多了三次项和四次项，但是通过加上惩罚项之后求出来的θ3和θ4就会很小，从而使曲线光滑趋近于二次曲线。

但是如果设置惩罚系数lamda过大的话，会出现所有的theta1,theta2......theta100,都会被小到忽略。

3.线性回归的正则化

在代价函数里加上了正则项，从而在递归下降求解时的公式也发生了改变，如下:

i表示第几个样本，j表示一个样本内的指标序号。

4.逻辑回归的正则化

逻辑回归梯度下降迭代时，即如图。

逻辑回归代价函数加上的惩罚项是lamda/2*m(Σtheta j ^2)。