BZOJ 1003: [ZJOI2006]物流运输（spfa+dp）

http://www.lydsy.com/JudgeOnline/problem.php?id=1003

题意：

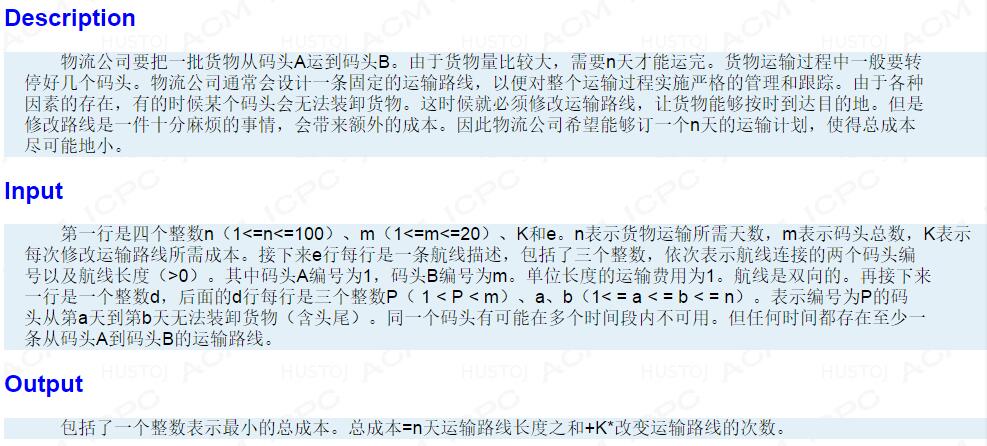
思路：

首先用spfa计算一下任意两天之内的最短路，dis[a][b]表示的就是在第a天~第b天从1到m的最短路。

接下来就是dp了，f[i]表示前i天的最小代价，那么状态转移方程就是：

f[i]=min(f[i],f[j]+dis[j+][i]*(i-j)+k)

注意：边界条件f[0]=-k！

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<sstream>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 #include<set>
 using namespace std;
 typedef long long ll;
 typedef pair<int,ll> pll;
 const int INF = 0x3f3f3f3f;
 const int maxn=+;

 int n, m, k, t;
 int tot;
 int head[maxn];
 int flag[maxn][maxn];
 int dis[maxn][maxn];
 int d[maxn];
 int inq[maxn];
 ll f[maxn];

 struct node
 {
     int v, w;
     int next;
 }e[maxn];

 void AddEdge(int u, int v, int w)
 {
     e[tot].v=v;
     e[tot].w=w;
     e[tot].next=head[u];
     head[u]=tot++;
 }

 void spfa(int s, int a, int b)
 {
     for(int i=;i<=m;i++)   d[i]=INF;
     queue<int> Q;
     Q.push(s);
     d[s]=;
     while(!Q.empty())
     {
         int u=Q.front(); inq[u]=; Q.pop();
         for(int i=head[u];i!=-;i=e[i].next)
         {
             int v=e[i].v;
             if(flag[v][b]-flag[v][a-]>)  continue;
             if(d[v]>d[u]+e[i].w)
             {
                 d[v]=d[u]+e[i].w;
                 if(!inq[v])
                 {
                     Q.push(v);
                     inq[v]=;
                 }
             }
         }
     }
     dis[a][b]=d[m];
 }

 int main()
 {
     //freopen("in.txt","r",stdin);
     while(~scanf("%d%d%d%d",&n,&m,&k,&t))
     {
         tot=;
         memset(head,-,sizeof(head));
         memset(flag,,sizeof(flag));
         for(int i=;i<t;i++)
         {
             int u,v,w;
             scanf("%d%d%d",&u,&v,&w);
             AddEdge(u,v,w);
             AddEdge(v,u,w);
         }

         scanf("%d",&t);
         while(t--)
         {
             int x,a,b;
             scanf("%d%d%d",&x,&a,&b);
             for(int i=a;i<=b;i++)  flag[x][i]=;
         }

         for(int i=;i<=m;i++)
             for(int j=;j<=n;j++)  flag[i][j]+=flag[i][j-];  //用前缀和可以快速判断i~j天是否可用
 94
         for(int i=;i<=n;i++)
             for(int j=i;j<=n;j++)  spfa(,i,j);

         f[] = -k;  //注意边界条件
         for(int i = ; i <= n; i ++)
         {
             f[i] = INF;
             for(int j = ; j < i; j++)
             f[i] = min(f[i], f[j] + 1LL*dis[j+][i]*(i-j) + k);
         }
         printf("%d\n",f[n]);
     }
     return ;
 }