java 环形链表实现约瑟夫（Joseph）问题

约瑟夫问题又名丢手绢问题。相传著名犹太历史学家 Josephus 利用其规则躲过了一场自杀游戏，而后投降了罗马。

问题：

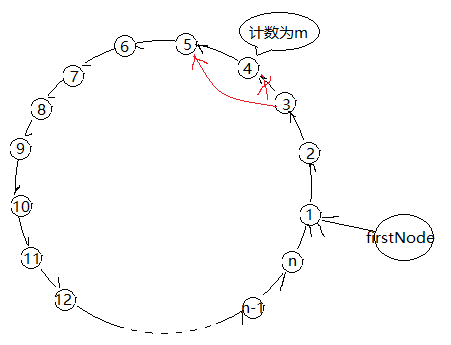
已知n个人（以编号1，2，3...n分别表示）围坐在一张圆桌周围。
* 从编号为k的人开始报数，数到m的那个人出列；
* 他的下一个人又从1开始报数，数到m的那个人又出列；
* 依此规律重复下去，直到圆桌周围的人全部出列。

用节点来模拟游戏中的人，用链表来表示游戏中的人按一定的顺序排列。每一个节点给一个编号，从编号为k的节点开始计数，计到m的节点从链表中退出。
之后m的下一个节点从新开始计数，依次...
计数为m的节点要被从链表中删除，只需要将m的上一个节点的引用指向m的下一个节点便可。
依上可知我们的节点类只需要两个属性，一个表示它自己的编号，另一个是引用，指向下一个节点，最后的节点指向第一个节点。
对于第一个节点必须要有一个入口节点————否则无法进入环形链表。

我们需要一个跑龙套的节点以便处理游戏中的计数。
由于是单向链表，所以当我们找到计数为m的节点时还要定位m的上一个节点，并更新其引用，使得计数为m的节点失去引用后被java垃圾回收机制处理掉。
要定义m的上一个节点，可以依链表方向，重新遍历一遍到一个引用指向计数为m的节点，该节点便是。
　　　　　　　　　　还可以将链表换成双向链表，也可以定义两个跑龙套的节点一个用以计数，一个随后以便定位m的上一个节点。
这些方法这里都不用，由于找到计数为m的节点并不需要对它做任何处理，而是处理它的上一个节点————将其引用更新为m的下一个节点，
所以我们可以简而计数到m-1便可直接处理。
给出完整代码如下：

public class JosephCycle {
    public static void main(String []args){
        CycleLink cl = new CycleLink();
        cl.setLen(7);
        cl.setK(3);
        cl.setM(3);
        cl.creatLink();
        cl.play();
        cl.show();
    }

}

class Node{
    int num;
    Node nextNode = null;
    public Node(int num){
        this.num = num;
    }
}

class CycleLink{
    int len;
    int k ;
    int m ;
    Node firstNode = null;
    Node temp = null;
    public void setLen(int len){
        this.len = len;
    }

    public void setK(int k){
        this.k = k;
    }
    public void setM(int m){
        this.m =m;
    }

    //创建链表
    public void creatLink(){
        for(int i = 1; i <= len ; i++){
            // 处理首节点
            if(i==1){
                Node  nd= new Node(i);
                firstNode = nd;
                temp = nd;
            }else if(i == len){    //处理末节点
                Node nd = new Node(i);
                temp.nextNode = nd;
                temp = nd;
                temp.nextNode = firstNode;
            }else{
                Node nd = new Node(i);
                temp.nextNode = nd;
                temp = nd;
            }
        }
    }

    public void play(){
        temp = firstNode;
        // 先找到编号为k的节点
        for(int i = 1 ; i < k; i++){
            temp = temp.nextNode;
        }
        while(this.len !=1){
            //报数，找到m的上一个节点
            for(int j = 1 ;j < m-1; j++){
                temp = temp.nextNode;
            }

            //因为少报了  1  ,所以将下一个节点删除,并从下下一个节点重新开始报数
            System.out.println("要删除的节点： "+temp.nextNode.num);
            /**
             * 如果删除节点是firstNode，则将firstNode更新为下一个节点
             * 注意不能用编号判断，因为新的编号对应的节点有可能又被删除
             */
            if(temp.nextNode==firstNode){
                firstNode = temp.nextNode.nextNode;
            }
            temp.nextNode = temp.nextNode.nextNode;
            temp = temp.nextNode;
            //this.show();
            this.len--;
        }

    }

    /**
     * 遍历链表打印整个链表
     */
    public void show(){
        temp = firstNode;
        do{
            System.out.println(temp.num);
            temp = temp.nextNode;
        }while(temp != firstNode);
    }
}    

这段代码可拿来直接运行，运行结果：

　　　　

最后剩余的节点为：6

在实际应用中，比如排队，根据不同的k，m，len的值，对于有些特殊情况，可能有不同的算法我也不知道，猜测如此！

为何有此猜想，读者可参看：约瑟夫环问题详解