MT【43】抛物线不常见性质2.
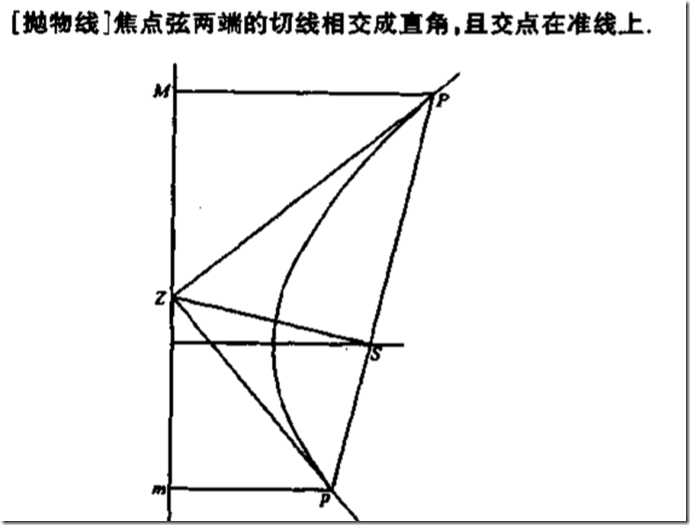

注:S为抛物线焦点
MT【43】抛物线不常见性质2.的更多相关文章
- MT【44】抛物线不常见性质3
注:S为抛物线的焦点
- MT【42】抛物线不常见性质1.
评:特别的,当$PP'$为切线时,$\angle PSK=90^0$ 注:S为抛物线焦点.
- MT【237】阿基米德三角形的一些常见性质
阿基米德三角形的常见性质:抛物线:$x^2=2py,AB$为抛物线的弦,$AQ,BQ$为切线,记$Q(x_0,y_0)$则$1)k_{QA}*k_{QB}=\dfrac{p}{2x_0}$$2)k_{ ...
- 【C++进阶:STL常见性质】
STL中的常用容器包括:顺序性容器(vector.deque.list).关联容器(map.set).容器适配器(queue.stac) 转载自:https://blog.csdn.net/u0134 ...
- 【C++进阶:STL常见性质3】
STL3个代表性函数:for_each(), random_shuffle(), sort() vector<int> stuff; random_shuffle(stuff.begin( ...
- 【C++进阶:STL常见性质2】
一般STL函数接收迭代器参数的规则为:[it1, it2) 左闭右开区间: vector<int> scores; scores.erase(scores.begin(),scores.e ...
- 【learning】莫比乌斯反演
吐槽 额其实这个东西的话..好像缠着机房里面的dalao们给我讲过好多遍了然后.. 拖到现在才搞懂也是服了qwq(可能有个猪脑子) 感觉就是主要几条式子然后疯狂换元换着换着就化简运算了? 草稿纸杀手q ...
- 线性回归(linear regression)
基本形式 最小二乘法估计拟合参数 最小二乘法:基于均方误差最小化来进行模型求解的方法称为“最小二乘法”(least square method) 即(左边代表 $\mathbf{\omega }$ 和 ...
- (暂时弃坑)(半成品)ACM数论之旅18---反演定理 第二回 Mobius反演(莫比乌斯反演)((づ ̄3 ̄)づ天才第一步,雀。。。。)
莫比乌斯反演也是反演定理的一种 既然我们已经学了二项式反演定理 那莫比乌斯反演定理与二项式反演定理一样,不求甚解,只求会用 莫比乌斯反演长下面这个样子(=・ω・=) d|n,表示n能够整除d,也就是d ...
随机推荐
- Linux_软件安装管理
开始学习rpm,yum等命令的使用,下面的地址可供你学习 大部分都大同小异! 感谢作者:https://segmentfault.com/a/1190000011200461
- C# 深浅复制 MemberwiseClone
学无止境,精益求精 十年河东,十年河西,莫欺少年穷 学历代表你的过去,能力代表你的现在,学习代表你的将来 最近拜读了大话设计模式:原型模式,该模式主要应用C# 深浅复制来实现的!关于深浅复制大家可参考 ...
- NOIP2018题解
Preface 联赛结束后趁着自己还没有一下子把题目忘光,所以趁机改一下题目. 没有和游记一起写主要是怕篇幅太长不美观. 因此这里我们直接讲题目,关于NOIP2018的一些心得和有趣的事详见:NOIP ...
- loj6062 pair
直接套用霍尔定理. 由于A有多个选择,考虑维护B是否合法. 首先B数组的顺序显然是没有用的,可以直接排序. 然后每个A就都变成了向一个后缀连边. 对于B,原本需要check每一个集合是否满足|u|&l ...
- 基于uFUN开发板的心率计(二)动态阈值算法获取心率值
前言 上一篇文章:基于uFUN开发板的心率计(一)DMA方式获取传感器数据,介绍了如何获取PulseSensor心率传感器的电压值,并对硬件电路进行了计算分析.心率计,重要的是要获取到心率值,本篇文章 ...
- Jmeter(三十三)_JsonPath表达式提取响应
我们在用jmeter做接口测试的时候,有的时候会遇到一些复杂的json响应.比如多层list嵌套时的取值 一个简单的例子: $..Name:列出所有省份 $..Province[0].Name 提取P ...
- SKINNY加密算法详解(无代码,仅加密)
原作者论文请参考<The SKINNY Family of Block Ciphers and Its Low-Latency Variant MANTIS> 地址为:https://li ...
- 测试网站页面网速的一个简单Python脚本
无聊之余,下面分享一个Python小脚本:测试网站页面访问速度 [root@huanqiu ~]# vim pywww.py #!/usr/bin/python # coding: UTF-8 imp ...
- nginx日志格式字段
Nginx日志主要分为两种:访问日志和错误日志.日志开关在Nginx配置文件(/etc/nginx/nginx.conf)中设置,两种日志都可以选择性关闭,默认都是打开的. 访问日志 访问日志主要记录 ...
- Echarts中graph类型的运用求教
以下是百度Echarts官网上关系图的源码,但是这个关系图的node节点和edge都是静态文件里规定好的,我现在想动态实现,点击其中一个节点A然后新产生一个新节点B,并且有A和B之间的edge,就类似 ...
