[leetcode]53. Maximum Subarray最大子数组和

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.

Example:

Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.

Follow up:

If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.

题意：

求最大子数组和

思路：

开一个一维dp

原理：任何数加负数肯定比原值小

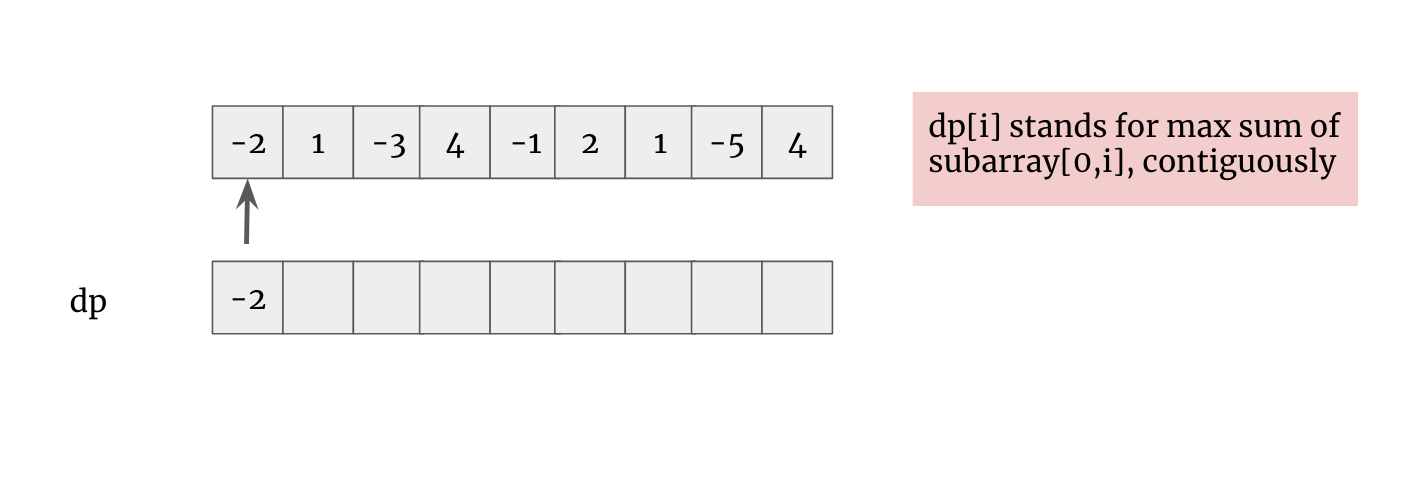
1. dp[i] stands for max sum of subarray[0,i] (nums[i] must be used)

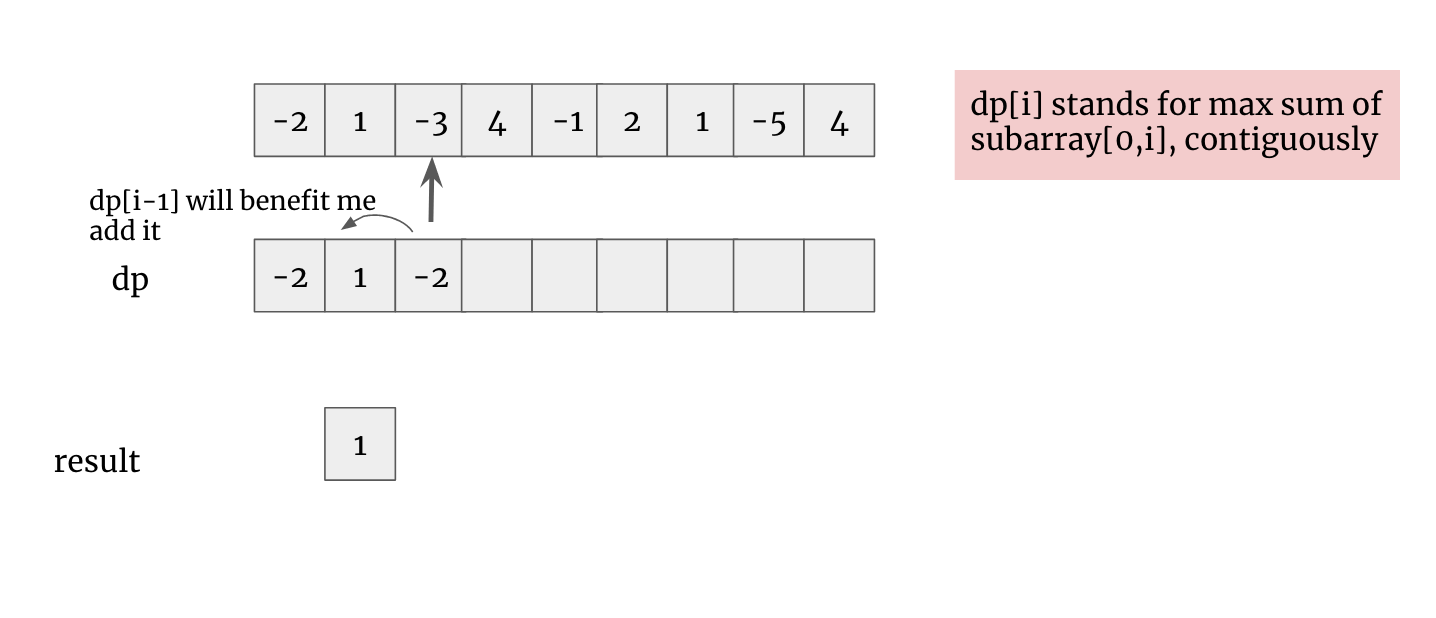
2. coz any negative will worsen final result.  supposing I am standing at current nums[i],  if previous sum dp[i-1]  > 0, it will benifit result, then we wrap dp[i-1] + nums[i] to dp[i]

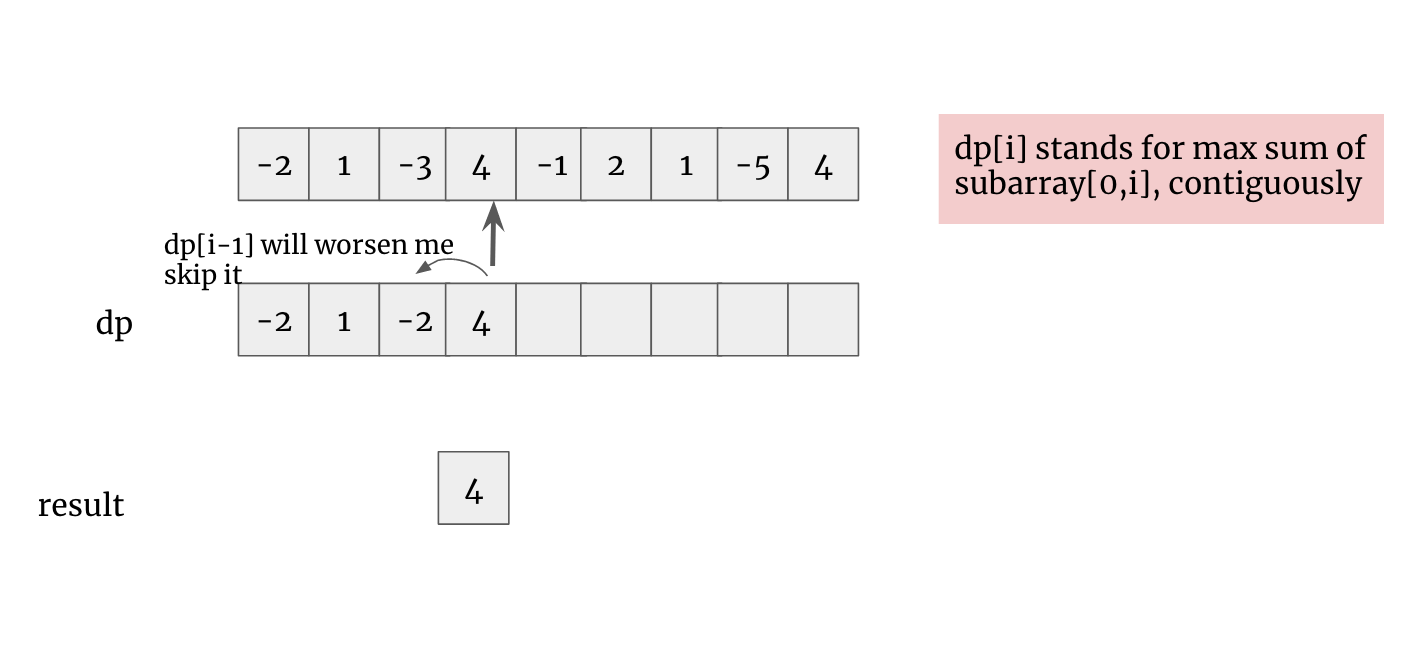
otherwise, if dp[i-1] < 0, we only keep nums[i]

3. the  dp function will be :

dp[i] = dp[i-1] >0 ? dp[i-1] + num[i] : num[i]

code

 class Solution {
     public int maxSubArray(int[] nums) {
         // dp[i]: max sum of subarray from 0 to i
         int[] dp = new int[nums.length];
         // initiliaze
         dp[0] = nums[0];
         int result = nums[0];

         for(int i = 1; i < nums.length; i++){
             // negative value will worsen result, if dp[i-1] < 0, we only keep nums[i]
             dp[i] = dp[i-1] > 0 ? dp[i-1] + nums[i] : nums[i];
             // update max result
             result = Math.max(result, dp[i]);
         }
        return result;
     }
 }

思路

优化空间为O(1)

Coz result is only related to previous sum.

We can use a variable to track previous sum.

代码

 public class MaximumSubarray {
     public int maxSubArray(int[] nums) {
         // initialize
         int result = Integer.MIN_VALUE;
         // reset it to 0 if it's less than 0.
         int sum = 0;
         for (int n : nums) {
             // if sum < 0, we only keep n; if sum > 0, sum to be added to benefit result
             sum = n + Math.max(sum, 0);
             // update max result
             result = Math.max(result, sum);
         }
         return result;
     }
 }