Code-force 1003 E Tree Constructing

                                                                                                E. Tree Constructing

You are given three integers nn, dd and kk.

Your task is to construct an undirected tree on nn vertices with diameter dd and degree of each vertex at most kk, or say that it is impossible.

An undirected tree is a connected undirected graph with n−1n−1 edges.

Diameter of a tree is the maximum length of a simple path (a path in which each vertex appears at most once) between all pairs of vertices of this tree.

Degree of a vertex is the number of edges incident to this vertex (i.e. for a vertex uu it is the number of edges (u,v)(u,v) that belong to the tree, where vv is any other vertex of a tree).

Input

The first line of the input contains three integers nn, dd and kk (1≤n,d,k≤4⋅1051≤n,d,k≤4⋅105).

Output

If there is no tree satisfying the conditions above, print only one word "NO" (without quotes).

Otherwise in the first line print "YES" (without quotes), and then print n−1n−1 lines describing edges of a tree satisfying the conditions above. Vertices of the tree must be numbered from 11 to nn. You can print edges and vertices connected by an edge in any order. If there are multiple answers, print any of them.1

题意：

　　要构建一颗树，树的直径要是d，就是树上的节点最远的距离为d，每个节点的度最多为k,一共有n个节点。

思路：

　　先判断可不可以建出符合要求的树，可以的话，先把直径建好，再到这条直径上挂上子树。

　　

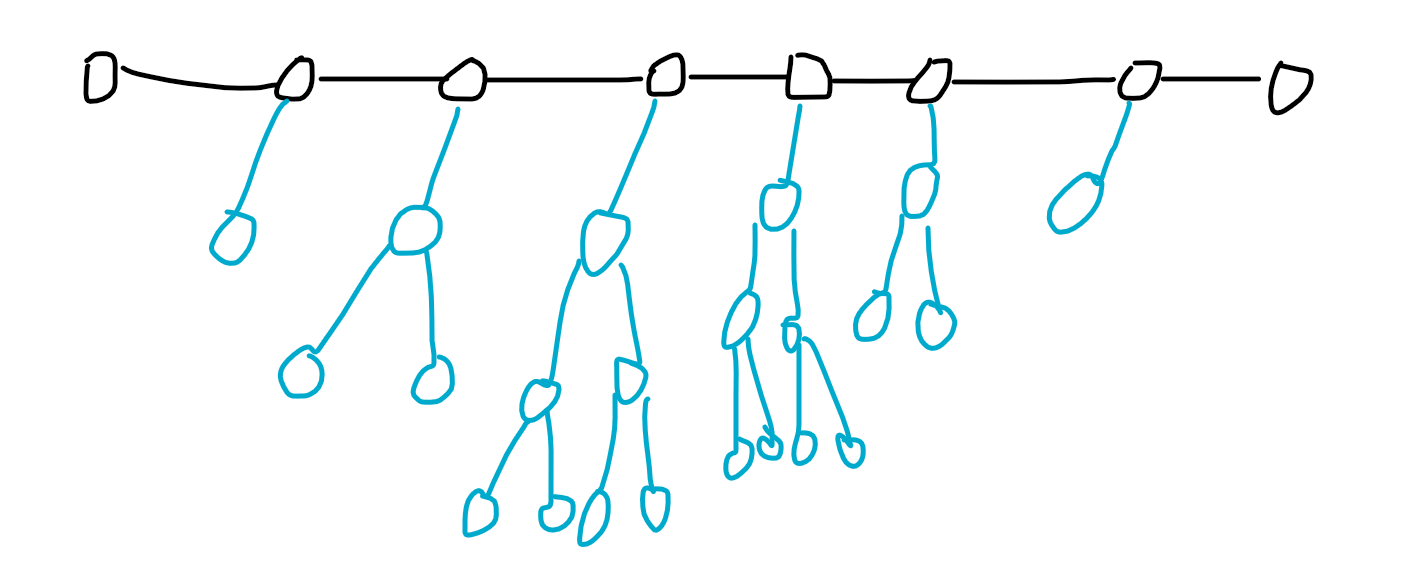
　　注意子树的深度变化，还有建树的过程中，并不一定是建的如此之满，所以当节点数用完时，要及时退出。

AC代码（C++）

#include<iostream>
#include<queue>
using namespace std;
int n,d,k,flag,t;
int quick_pow(int a,int b)
{
    int ans=0,t=1;
    for(int i=0;i<b;i++){
        t*=a;
        ans+=t;
        if(ans>=n){return -1;}
    }
    return ans;
}

void build(int s,int h,int de)//de是子树的深度，s是父节点
{
    if(h>de){return;}
    if(t>=n){return;}
    t++;
    printf("%d %d\n",s,t);
    if(t>=n){return;}
    int o=t;
    if(h>de-1){return;}
    for(int i=0;i<k-1;i++){
        build(o,h+1,de);
        if(t>=n){return;}
    }
}

int main()
{
    scanf("%d%d%d",&n,&d,&k);
    if(n<d+1){printf("NO");return 0;}
    if(d&1){
        t=quick_pow(k-1,d/2);
        if(t==-1){printf("YES\n");}
        else{
            t=2*(t+1);
            if(t<n){printf("NO");return 0;}
        }
    }
    else {
        t=quick_pow(k-1,d/2-1);
        if(t==-1){printf("YES\n");}
        else{
            t=k*t+1+k;
            if(t<n){printf("NO");return 0;}
        }
    }
    if(t!=-1){printf("YES\n");}
    int de=-1;
    t=d+1;
    for(int i=1;i<=d;i++){
        printf("%d %d\n",i,i+1);
        if(t>=n){continue;}
        if(d&1){
            if(i<=d/2+1){de++;}
            else if(i>d/2+2){de--;}
        }
        else {
            if(i<=d/2+1){de++;}
            else de--;
        }
        for(int j=0;j<k-2;j++){
            build(i,1,de);if(t>=n){break;}
        }
    }
}