【洛谷P1962】斐波那契数列

斐波那契数列

题目链接：https://www.luogu.org/problemnew/show/P1962

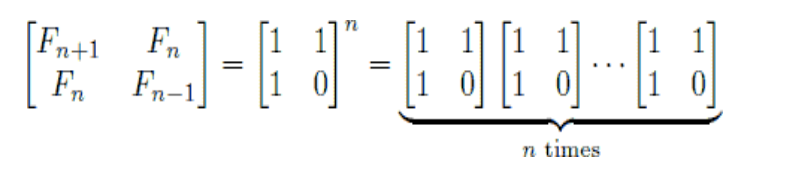
矩阵A

1,1

1,0

用A^k即可求出feb（k）。

矩阵快速幂

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 long long n=,k;
 const long long MOD=;
 struct Matrix{
     long long m[][];
 };
 Matrix A,E,K;

 Matrix cheng(Matrix X,Matrix Y)
 {
     Matrix C;
     for(long long i=;i<=n;i++)
      for(long long j=;j<=n;j++)
      {
          C.m[i][j]=;
          for(long long l=;l<=n;l++)
              C.m[i][j]=(C.m[i][j]+(X.m[i][l]*Y.m[l][j]))%MOD;
      }
      return C;
 }
 Matrix qsort(Matrix X,long long p)
 {
     Matrix S=E;
     while(p)
     {
         if(p&) S=cheng(S,X);
         X=cheng(X,X);
         p>>=;
     }
     return S;
 }
 int main()
 {
     scanf("%lld",&k);
     E.m[][]=;
     E.m[][]=;
     A.m[][]=;
     A.m[][]=;
     A.m[][]=;
     K=qsort(A,k);
     printf("%lld\n",K.m[][]);
     return ;
 }