关于Topsort

Long time no see.

拓扑排序

英文名称：Topological-sort

别称：toposort or  topsort

拓扑排序是干什么的呢

对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

以上来自360百科

看明白了吗，反正我是不想看

正题

首先，我们由一个小问题引入。

有这么一群小黄人，小红爱着小绿，她得亲眼看着小绿吃完饭她才会安心吃饭，

而这个时候，小黄也爱着小绿，他也要亲眼看着小绿把饭吃完她才会安心。

同时，小蓝爱着小红和小黄，她得亲眼看着小红和小黄吃完饭她才可以吃饭，

而小紫是个基佬，他不爱小红，不爱小黄，不爱小蓝，也不爱小绿，正因为他是基佬所以他对小红小黄毫无威胁性，

于是小紫可以同小绿一起吃饭，当然也不可以不。

那么最终，大家吃饭的顺序是怎样的呢。

形象一点，画个图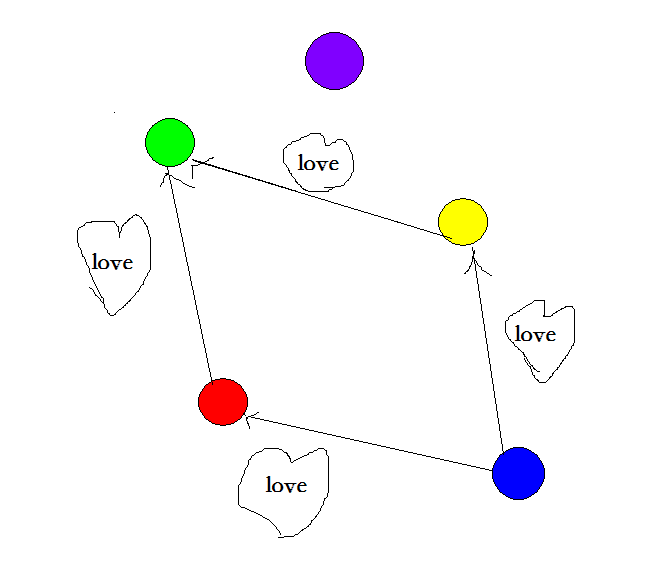

也许对于一些大佬们他们可能会想：这个sb题！这不是分分钟秒切的事情吗！

我：爆搜？？

显然，

数据大了就不行了。

们首先讲的，是Kahn算法

其算法主要流程如下：

1.从图中找到一个入度为零的点，并输出

2.在图中删去和这个点相连的所有边，再重复1的操作

3.一直重复1.2的操作一直到图中不再有入度不为零的点为止。

当然，如果图中有环那是无解的。

那么它的时间复杂度是多少呢？

证明：初始化入度为0的集合需要遍历整张图，检查每个节点和每条边，对该集合进行操作，又需要遍历整张图中的，每条边，则复杂度为O(E+V);

代码:

#include <stack>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn =  + ;
const int INF = 1e9 + ;
int T, n, m, num[maxn];
vector<int> vis[maxn], v;
stack<int> s;
void topo() {
    for(int i = ; i <= n; i++)
        if(num[i] == ) s.push(i);
    while(!s.empty()) {
        int now = s.top();
        v.push_back(now);
        s.pop();
        for(int j = ; j < vis[now].size(); j++)
            if((--num[vis[now][j]]) == )
                s.push(vis[now][j]);
    }
    if(v.size() != n) cout << "NO solution" << '\n';
    else for(int i = ; i < v.size(); i++) cout<<v[i]<<" ";
}
int main() {
    scanf("%d%d", &n, &m);
    for(int i = ;  i <= n; i++) vis[i].clear();
    memset(num, , sizeof(num));
    for(int i = , u, v; i < m; i++)
        scanf("%d%d", &u, &v), vis[u].push_back(v), num[v]++;
    topo();
    return ;
}

现在我们再来讲基于DFS的算法

需要注意的是，将顶点添加到结果anst中的时机是在vis方法即将退出之时。

搜索嘛，实践略简单，但是理解上要下点功夫。

其关键在于为什么在vis方法的最后将该顶点添加到一个集合中，就能保证这个集合就是拓扑排序的结果？

因为添加顶点到集合中的时机是在dfs方法即将退出之时，而dfs方法本身是个递归方法，只要当前顶点还存在边指向其它任何顶点，它就会递归调用dfs方法，而不会退出。因此，退出dfs方法，意味着当前顶点没有指向其它顶点的边了，即当前顶点是一条路径上的最后一个顶点。

那么问题来了，这个方法对吗？

证明：

考虑任意的边，当调用dfs(v)的时候，有三种情况：

• dfs(w)还没有被调用，即所要走的点还未走，此时会调用dfs(w)，然后当dfs(w)返回之后，dfs(v)才会返回
• dfs(w)已经被调用并返回了，即w已经被mark
• dfs(w)已经被调用但是在此时调用dfs(v)的时候还未返回

需要注意的是，以上第三种情况在拓扑排序的场景下是不可能发生的，因为如果情况3是合法的话，就表示存在一条由w到v的路径。而现在我们的前提条件是由v到w有一条边，这就导致我们的图中存在环路，从而该图就不是一个有向无环图(DAG)，而我们已经知道，非有向无环图是不能被拓扑排序的。

那么考虑前两种情况，无论是情况1还是情况2，w都会先于v被添加到结果列表中。所以边v->w总是由结果集中后出现的顶点指向先出现的顶点。为了让结果更自然一些，可以使用栈来作为存储最终结果的数据结构，从而能够保证边v->w总是由结果集中先出现的顶点指向后出现的顶点。

时间复杂度：

证明：DFS遍历一遍的时间为O(E+V)，而记录结果的时间花费为O(1)，所以总时间复杂度为O(E+V)

代码：

#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn =  + ;
const int INF = 1e9 + ;
int n, m, dis[maxn], ans[maxn], t;
vector<int> vis[maxn];
bool dfs(int u) {
    dis[u] = -;
    for(int i = ; i < vis[u].size(); i++) {
        int v = vis[u][i];
        if(dis[v] < ) return false;
        else if(!dis[v] && !dfs(v)) return false;
    }
    dis[u] = , ans[--t] = u;
    return true;
}
bool toposort() {
    t = n;
    memset(dis, , sizeof(dis));
    for(int u = ; u <= n; u++)
        if(!dis[u]) if(!dfs(u)) return false;
    return true;
}
int main() {
    scanf("%d%d", &n, &m);
    for(int i = ;  i <= n; i++) vis[i].clear();
    for(int i = , u, v; i < m; i++)
        scanf("%d%d", &u, &v), vis[u].push_back(v);
    if(toposort()) for(int i = ; i < n; i++) printf("%d ",ans[i]);
    else puts("NO solution");
    return ;
}

等一朵花开，换一世情怀