PAT_A1135#Is It A Red-Black Tree

Source:

PAT A1135 Is It A Red-Black Tree (30 分)

Description:

There is a kind of balanced binary search tree named red-black tree in the data structure. It has the following 5 properties:

• (1) Every node is either red or black.
• (2) The root is black.
• (3) Every leaf (NULL) is black.
• (4) If a node is red, then both its children are black.
• (5) For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.

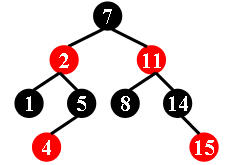
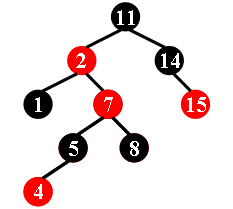
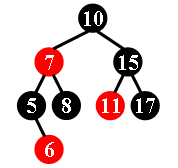
For example, the tree in Figure 1 is a red-black tree, while the ones in Figure 2 and 3 are not.

Figure 1	Figure 2	Figure 3

For each given binary search tree, you are supposed to tell if it is a legal red-black tree.

Input Specification:

Each input file contains several test cases. The first line gives a positive integer K (≤30) which is the total number of cases. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the preorder traversal sequence of the tree. While all the keys in a tree are positive integers, we use negative signs to represent red nodes. All the numbers in a line are separated by a space. The sample input cases correspond to the trees shown in Figure 1, 2 and 3.

Output Specification:

For each test case, print in a line "Yes" if the given tree is a red-black tree, or "No" if not.

Sample Input:

3
9
7 -2 1 5 -4 -11 8 14 -15
9
11 -2 1 -7 5 -4 8 14 -15
8
10 -7 5 -6 8 15 -11 17

Sample Output:

Yes
No
No

Keys:

• 二叉查找树（Binary Search Tree）

Attention:

• 应该注意到，红黑树（ balanced binary search tree）并不是AVL树（self-balancing binary search tree），英文题描述题这里很容易产生误解；
• 结点数目较少，给出先序遍历时，可以采用插入建树的方法；再次提醒，数据量较大时，会超时；
• 根结点的父亲预设为负值，即为红色。这样从根结点遍历时，不必特判性质2，由性质4可以推出性质

Code:

 /*
 Data: 2019-06-26 15:30:16
 Problem: PAT_A1135#Is It A Red-Black Tree
 AC: 23:52

 题目大意：
 红黑树具有如下性质的平衡二叉树（非AVL树）：
 1.结点非红即黑
 2.根结点为黑色
 3.叶子结点（空结点）为黑色
 4.红色结点的孩子均为黑色
 5.任意结点到叶子结点构成的简单路径所含的黑色结点数目相同
 现给定一棵二叉树，判定其是否为红黑树
 输入：
 第一行给出，测试数K<=20
 第二行给出，结点总数N<=30
 第三行给出，先序遍历，键值均正，负数表示红色结点

 基本思路：
 建树，遍历一次二叉树
 根据当前结点与父结点的关系，判断性质2,4
 统计各结点左子树与右子树的黑色结点个数（类似于计算AVL树的平衡因子）
 若相等，则符合性质5，并根据当前结点颜色，返回黑色结点个数
 */
 #include<cstdio>
 #include<cmath>
 using namespace std;
 struct node
 {
     int data;
     node *lchild,*rchild;
 };

 void Insert(node *&root, int x)
 {
     if(root == NULL)
     {
         root = new node;
         root->data = x;
         root->lchild = root->rchild = NULL;
     }
     else if(abs(x) < abs(root->data))
         Insert(root->lchild, x);
     else
         Insert(root->rchild, x);
 }

 int Travel(node *root, int father, int &ans)
 {
     if(ans== || root==NULL)
         return ;
     int l = Travel(root->lchild, root->data, ans);
     int r = Travel(root->rchild, root->data, ans);
     if(l!=r || (father< && root->data<)){
         ans=;
         return ;
     }
     if(root->data<)
         return l;
     else
         return l+;
 }

 int main()
 {
 #ifdef ONLINE_JUDGE
 #else
     freopen("Test.txt", "r", stdin);
 #endif // ONLINE_JUDGE

     int n,m,x;
     scanf("%d", &m);
     while(m--)
     {
         node *root = NULL;
         scanf("%d", &n);
         for(int i=; i<n; i++)
         {
             scanf("%d", &x);
             Insert(root, x);
         }
         int ans=;
         Travel(root,-,ans);
         if(ans)
             printf("Yes\n");
         else
             printf("No\n");
     }

     return ;
 }