NOI 2011 【阿狸的打字机】

之前讲了【AC自动姬】，今天我终于把这题给刚下来了。。。嗯，来给大家讲一讲。

题目描述：

打字机上只有28个按键，分别印有26个小写英文字母和'B'、'P'两个字母。经阿狸研究发现，这个打字机是这样工作的：

输入小写字母，打字机的一个凹槽中会加入这个字母(这个字母加在凹槽的最后)。

按一下印有'B'的按键，打字机凹槽中最后一个字母会消失。

按一下印有'P'的按键，打字机会在纸上打印出凹槽中现有的所有字母并换行，但凹槽中的字母不会消失。

例如，阿狸输入aPaPBbP，纸上被打印的字符如下：

a aa ab

我们把纸上打印出来的字符串从1开始顺序编号，一直到n。打字机有一个非常有趣的功能，在打字机中暗藏一个带数字的小键盘，在小键盘上输入两个数(x,y)（其中1≤x,y≤n），打字机会显示第x个打印的字符串在第y个打印的字符串中出现了多少次。

阿狸发现了这个功能以后很兴奋，他想写个程序完成同样的功能，你能帮助他么？

思路分析：

　　四十分算法大家都知道吧？对于每一个询问都跑KMP就行了。

　　正解应该和AC自动机有关，这也应该没问题吧。

那就给大家讲两个恐怖故事吧：

这道题目，把每一个字符串都存下来会超内存。

这道题目，把每一个字符串都按照原先的方式插入trie树会超时。

嗯，听完这两个恐怖故事是不是瑟瑟发抖呢？（如果没有，那就********

那么我们先来讲一讲上面问题的处理方式吧。

看一看阿狸的打字机的运行方式，每次都不会清空，一次只加一个字符，删除也就删一个字符，想到了什么？——我们能不能一边读入，一边构造trie树呢，记录下每个单词的最后一个节点，不就可以倒着向上走，还原出各个单词了吗？

嗯，非常好，上面的两个问题就这样被我们完美解决掉了！（鼓掌

然后我们应该怎么做呢？

观察询问——第x个字符串在第y个字符串中出现了几次。

想一想，在AC自动机上，假如说，一个字符串在另一个字符串中出现会发生什么（假如说是两个字符串“shehe”和“he”）

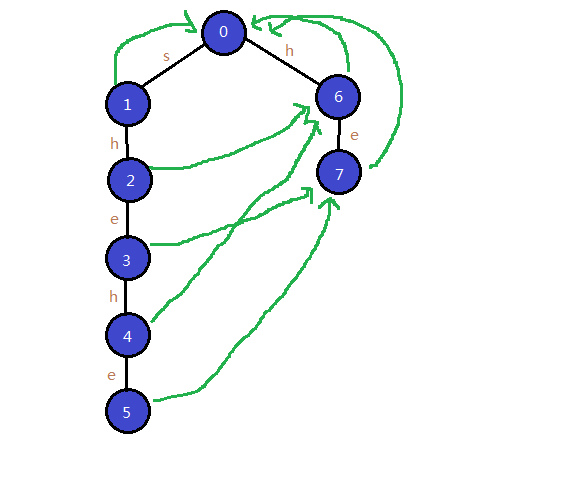（手画的，有点难看。。。绿色的边是fail指针）

我们发现，当he在shehe中出现时，出现he的节点3和5，fail指针都指向了7号点he。

这是为什么呢？

回顾我们上篇在强调的——fail指针指向的是当前串的部分后缀与其它模式串的前缀完全相同 的节点。

也就是说，包含he的字符串，肯定可以通过fail指针若干次跳转，来到he的节点（就是图中的7号点）。因为，它（指图中的3、5号点）有部分后缀是和he这个串的前缀完全相同的。

那么我们把所有trie树的边去掉，只留下fail指针，这样也会构成一颗树对吧，我们叫它fail树。（如下图）

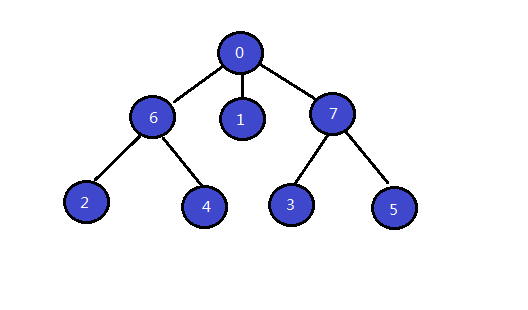
也就是说，我们想要求出x字符串在y字符串中出现了几次，只需要统计fail树上，有多少属于y字符串的节点在以x字符串的结束节点为根的子树里就行了。

树上统计问题，想到了什么？——DFS序嘛！

因为以x字符串的结束节点为根的子树在dfs序上是连续的，所以我们肯定不能把它作为突破口，因为它肯定可以在log n的时间内求解（推荐用树状数组），没有必要再去对它进行讨论。

把问题进行转换——统计trie树上从根到y字符串结束节点的路径上有多少节点在fail树上是在以x字符串的结束节点为根的子树中的。

很容易想到把询问都离线出来，然后按照y归类，因为只要y相等的话，那么就可以一次性，把每个询问在log n的时间内求出来。

这样，问题就变得简单了，因为以x字符串的结束节点为根的子树在dfs序上是连续的，所以我们只要维护好从根到y字符串结束节点的路径上的节点就可以了。

其实这个东西我们也可以跟着读入的那一大坨，进行维护。

每加入一个节点就可以在trie树上走到那个节点，并且在树状数组中给它对应的dfn上+1。遇到‘B’时，就在树状数组中把之前加的1减掉，这样我们就可以保证树状数组中，只有trie树上从根到y字符串结束节点的路径上的节点在fail树上对应的dfn（貌似有点拗口），是有1的。

代码实现：

#include <bits/stdc++.h>
using namespace std;
const int maxn=100005;
char st[maxn];
string s[maxn];
vector <int> a[maxn],b[maxn];
int nxt[maxn*2],vet[maxn*2],head[maxn],trie[maxn][30],fail[maxn],his[maxn];
int dfn[maxn],end[maxn],c[maxn],ans[maxn],id[maxn],q[maxn],cnt,tot,tim,n,m,len,now;
void build(){
    int head=0,tail=0;
    for (int i=0;i<26;++i) if (trie[0][i]) q[++tail]=trie[0][i];
    while (head!=tail){
        int now=q[++head];
        for (int i=0;i<26;++i)
            if (trie[now][i])
                q[++tail]=trie[now][i],fail[trie[now][i]]=trie[fail[now]][i];
            else trie[now][i]=trie[fail[now]][i];
    }
}
void add(int x,int y){
    ++tot;
    nxt[tot]=head[x];
    vet[tot]=y;
    head[x]=tot;
}
void dfs(int u){
    dfn[u]=++tim;
    for (int i=head[u];i;i=nxt[i]) dfs(vet[i]);
    end[u]=tim;
}
void update(int x,int val){
    if (x<=tim) c[x]+=val,update(x+(x&-x),val);
}
int getsum(int x){
    if (x>0) return c[x]+getsum(x-(x&-x));
    return 0;
}
int main(){
    scanf("%s",st);
    for (int i=0;st[i];i++)
        if (st[i]=='B') now=his[--tot];
        else
            if (st[i]=='P') id[++n]=now;
            else {
                if (!trie[now][st[i]-'a']) trie[now][st[i]-'a']=++cnt;
                now=trie[now][st[i]-'a']; his[++tot]=now;
            }
    build(); tot=0;
    for (int i=1;i<=cnt;++i) add(fail[i],i);
    scanf("%d",&m); int x,y;
    for (int i=1;i<=m;++i)
        scanf("%d%d",&x,&y),a[id[y]].push_back(id[x]),b[id[y]].push_back(i);
    dfs(0); int u=0,tot=0;
    memset(his,0,sizeof(his));
    for (int i=0;st[i];i++)
        if (st[i]=='B') update(dfn[u],-1),u=his[--tot];
        else
            if (st[i]=='P') {
                int siz=a[u].size();
                for (int j=1;j<=siz;j++)
                    ans[b[u][j-1]]=getsum(end[a[u][j-1]])-getsum(dfn[a[u][j-1]]-1);
            }
            else u=trie[u][st[i]-'a'],his[++tot]=u,update(dfn[u],1);
    for (int i=1;i<=m;++i) printf("%d\n",ans[i]);
    return 0;
}