js 十大排序算法 All In One
js 十大排序算法 All In One
快速排序
归并排序
选择排序
插入排序
冒泡排序
希尔排序
桶排序
堆排序(二叉树排序)
基数排序
计数排序
堆排序(二叉树排序)
https://www.cnblogs.com/xgqfrms/p/13947103.html
refs
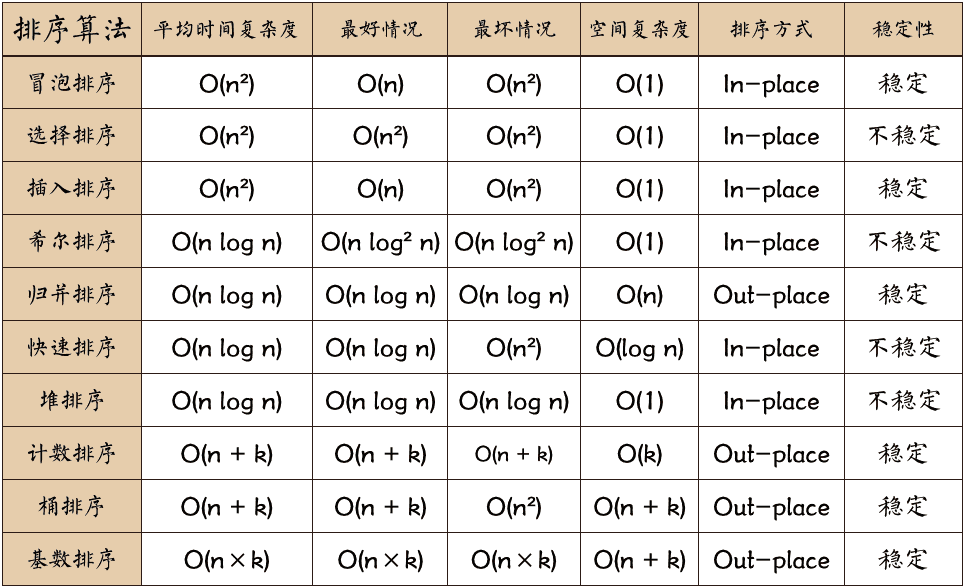
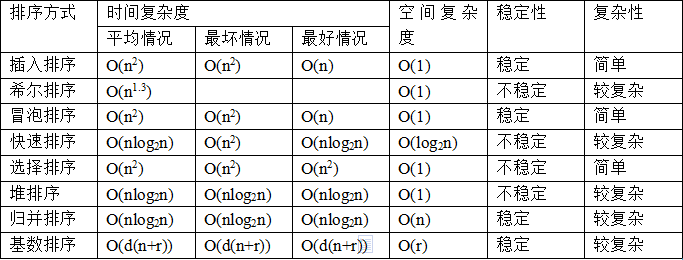
排序算法时间复杂度 bigO
https://www.cnblogs.com/xgqfrms/p/12927226.html
https://www.programmersought.com/article/42352705/
https://www.programmersought.com/article/757763614/
https://www.runoob.com/w3cnote/ten-sorting-algorithm.html
https://www.cnblogs.com/onepixel/articles/7674659.html
xgqfrms 2012-2020
www.cnblogs.com 发布文章使用:只允许注册用户才可以访问!
js 十大排序算法 All In One的更多相关文章
- [ 转载 ] js十大排序算法:冒泡排序
js十大排序算法:冒泡排序 http://www.cnblogs.com/beli/p/6297741.html
- js十大排序算法详解
十大经典算法导图 图片名词解释:n: 数据规模k:“桶”的个数In-place: 占用常数内存,不占用额外内存Out-place: 占用额外内存 1.冒泡排序 1.1 原始人冒泡排序 functi ...
- js十大排序算法收藏
十大经典算法排序总结对比 转载自五分钟学算法&https://www.cnblogs.com/AlbertP/p/10847627.html 一张图概括: 主流排序算法概览 名词解释: n: ...
- js十大排序算法
排序算法说明: (1)对于评述算法优劣术语的说明 稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面:不稳定:如果a原本在b的前面,而a=b,排序之后a可能会出现在b的后面: 内排序:所有排 ...
- js十大排序算法:冒泡排序
排序算法说明: (1)对于评述算法优劣术语的说明 稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面:不稳定:如果a原本在b的前面,而a=b,排序之后a可能会出现在b的后面: 内排序:所有排 ...
- 使用 js 实现十大排序算法: 快速排序
使用 js 实现十大排序算法: 快速排序 QuickSort 快速排序 /** * * @author xgqfrms * @license MIT * @copyright xgqfrms * @c ...
- 使用 js 实现十大排序算法: 归并排序
使用 js 实现十大排序算法: 归并排序 归并排序 refs js 十大排序算法 All In One https://www.cnblogs.com/xgqfrms/p/13947122.html ...
- 十大排序算法时间复杂度 All In One
十大排序算法时间复杂度 All In One 排序算法时间复杂度 排序算法对比 Big O O(n) O(n*log(n)) O(n^2) 冒泡排序 选择排序 插入排序 快速排序 归并排序 基数排序 ...
- 使用 js 实现十大排序算法: 桶排序
使用 js 实现十大排序算法: 桶排序 桶排序 refs xgqfrms 2012-2020 www.cnblogs.com 发布文章使用:只允许注册用户才可以访问!
随机推荐
- 在OpenDaylight controller上开发App
安装环境:Ubuntu18.04 一.安装依赖 1. 安装JDK: sudo apt update sudo apt install openjdk-8-jdk-headless 选择默认的 JDK: ...
- LVS负载均衡IP隧道模式原理介绍以及配置实战
LVS 基本工作原理 当用户向负载均衡调度器(Director Server)发起请求,调度器将请求发往至内核空间 PREROUTING 链首先会接收到用户请求,判断目标 IP 确定是本机 IP,将数 ...
- The router relies on a tree structure which makes heavy use of common prefixes, it is basically a compact prefix tree (or just Radix tree).
https://github.com/julienschmidt/httprouter/
- Architecture and design 洋葱 中间件 装饰器
Go kit - Frequently asked questions https://gokit.io/faq/ Architecture and design Introduction - Und ...
- 字节跳动在 Go 网络库上的实践
https://mp.weixin.qq.com/s/wSaJYg-HqnYY4SdLA2Zzaw RPC 框架作为研发体系中重要的一环,承载了几乎所有的服务流量.本文将简单介绍字节跳动自研网络库 n ...
- https://learnku.com/docs/go-blog/qihoo/6532 。 heap size went up to 69G, with maximum garbage collection (GC)
https://learnku.com/docs/go-blog/qihoo/6532 Use a Task Pool, a mechanism with a group of long-lived ...
- file descriptor 0 1 2 一切皆文件 stdout stderr stdin /dev/null 沉默是金 pipes 禁止输出 屏蔽 stdout 和 stderr 输入输出重定向 重定向文件描述符
movie.mpeg.001 movie.mpeg.002 movie.mpeg.003 ... movie.mpeg.099 $cat movie.mpeg.0*>movie.mpeg ...
- UVA11694 Gokigen Naname题解
目录 写在前面 Solution Code 写在前面 UVA的题需要自己读入一个 \(T\) 组数据,别被样例给迷惑了 Solution 每个格子只有两种填法且 \(n \le 7\),暴力搜索两种填 ...
- Jenkins免密码登录
Jenkins免密码登录 相关内容原文地址: 简书:海边的卡夫卡丶:Jenkins免密码登录 昨天惊现一个神奇的问题,Jenkins无法登录,无论是初始化的账号密码,还是admin用户,都登录不进去了 ...
- Centos搭建spark
Centos搭建spark 一.spark介绍 二.spark安装前提 三.集群规划 四.spark安装 五.修改spark环境变量 六.修改spark-env.sh 七.修改slaves 八.将安装 ...
