Just an Old Puzzle(2019多校1007)

Problem Description

You are given a 4 × 4 grid, which consists of 15 number cells and an empty cell.
All numbers are unique and ranged from 1 to 15.
In this board, the cells which are adjacent with the empty cell can move to the empty cell.
Your task is to make the input grid to the target grid shown in the figure below.
In the following example (sample input), you can get the target grid in two moves.

 

Input

The first line contains an integer T (1 <= T <= 10^5) denoting the number of test cases.
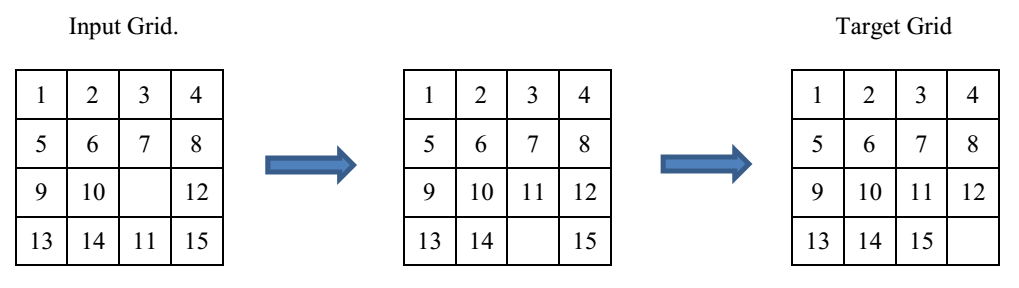
Each test case consists of four lines each containing four space-separated integers, denoting the input grid. 0 indicates the empty cell.

 

Output

For each test case, you have to print the answer in one line.
If you can’t get the target grid within 120 moves, then print 'No', else print 'Yes'.

 

Sample Input

2
1 2 3 4
5 6 7 8
9 10 0 12
13 14 11 15
1 2 3 4
5 6 7 8
9 10 11 12
13 15 14 0

 

Sample Output

Yes No

结论：拼图可解问题：当前空白的行距的奇偶性与当前序列的逆序数的奇偶性的抑或值来判断

代码：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<vector>
#include<cmath>

const int maxn=1e5+;
typedef long long ll;
using namespace std;
int a[];
int cc[];
int main()
{
    int T;
    cin>>T;
    int k=;

    while(T--)
    {
        int cnt=;
        for(int t=;t<;t++)
        {
            for(int j=;j<;j++)
            {
                scanf("%d",&a[t*+j]);
                if(a[t*+j]!=)
                {
                    cc[cnt++]=a[t*+j];
                }
                if(a[t*+j]==)
                {
                    k=t;
                }
            }
        }
    int sum=;
    for(int t=;t<;t++)
    {
        for(int j=t+;j<;j++)
        {
            if(cc[j]<cc[t])
            {
                sum++;
            }
        }
    }

    if(((-k)%)^(sum%)==)
    {
        puts("Yes");
    }
    else
    {
        puts("No");
    }
    }
    return ;
}