算法-搜索（3）AVL树

AVL树高度平衡的二叉搜索树，任一点的平衡印章只能是+1、-1、0，从而尽量降低树的高度。

如果它有n个结点，高度可保持在O(log₂n)，平均搜索长度也可保持在O(log₂n)。

（1）AVL树的插入

在插入一个新结点时，需要从插入位置沿通向根的路径回溯，检查各结点左右子树高度差。

发现结点的平衡因子为0，刚刚是在其较矮的子树插入新结点，从该结点到根的路径上各结点为根的子树高度不变、平衡因子不变，无需继续检查。

发现结点平衡因子|bf|=1，说明插入前是0，插入后该结点没有失去平衡。但该子树高度增加了，还需要继续往根方向检查。

发现某一结点|bf|=2不平衡，停止回溯，做平衡化旋转。

从发生不平衡的结点起，沿刚才回溯的路径取直接下两层的结点。

1.这三个结点位于同一条直线上，采用单旋转进行平衡化

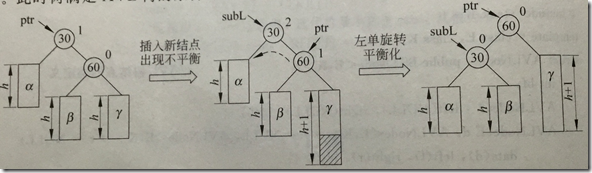
bf=2，右子树高，查看右结点bf=1，执行左单旋转

执行后ptr和subL的bf均变为0：

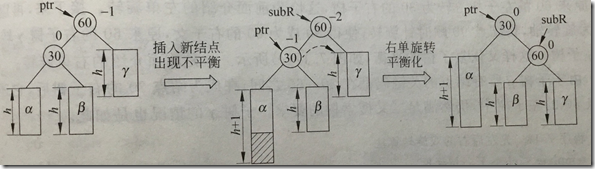
bf=-2，左子树高，查看左结点bf=-1，执行右单旋转

执行后ptr和subL的bf均变为0

2.这三个结点位于一条折线上，采用双旋转进行平衡化

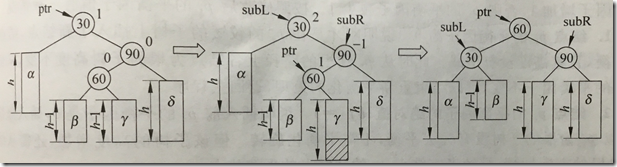
bf=2，右子树高，查看右结点bf=-1，无论ptr->bf是1还是-1，都执行先右后左双旋转

如果ptr的bf原为1，右单旋转后subR的bf改为0，先右后左双旋转，旋转后subL的bf变为-1

如果ptr的bf原为-1，右单旋转后subR的bf改为1，先右后左双旋转，旋转后subL的bf变为0

ptr的bf最终变为0

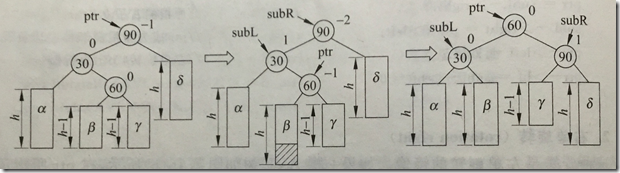
bf=-2，左子树高，查看左结点bf=1，无论ptr->bf是1还是-1，都执行先左后右双旋转

如果ptr的bf原为-1，左单旋转后subL的bf改为0，先左后右双旋转，旋转后subR的bf变为1

如果ptr的bf原为1，左单旋转后subL的bf改为-1，先左后右双旋转，旋转后subR的bf变为0

ptr的bf最终变为0

（2）AVL树的删除

1.被删结点有两个子女

寻找被删结点p在中序下的直接前驱或者直接后继q，把q的值给结点p，然后把结点q删除（q最多一个子女）

2.被删结点最多一个子女q

直接把p的父结点pr中原来指向p的指针指向q。

q是pr的左子女的话，pr的bf加1；q是pr的右子女的话，pr的bf减1。

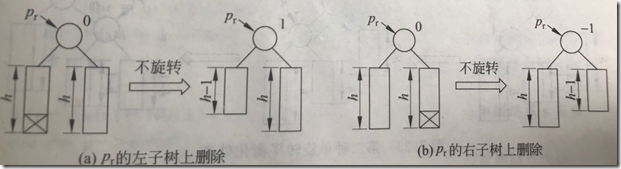
（1）pr的bf原为0，左/右子树被缩短后改为1/-1，以pr为根的子树高度未变，pr到根结点的路径上所有结点都不需要调整。

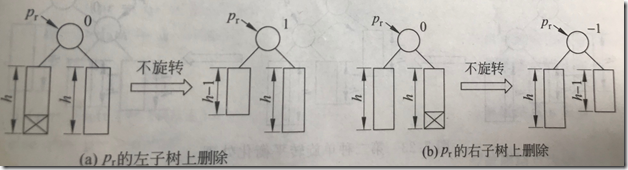
（2）pr的bf原不为0，较高的子树被缩短，bf变为0。

以pr为根的子树虽然平衡，但高度减少了。需要继续考察其父结点。

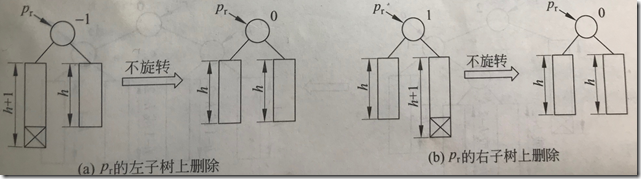
（3）pr的bf原不为0，较矮的子树又被缩短，bf变为±2。令q指向pr的较高的子树

①q->bf==0的情况：

pr的bf=2，右子树较高，右子树q的bf为0，作左单旋转

旋转后q->bf=pr->bf=0，还要把q->pf改为-1，pr->bf改为1

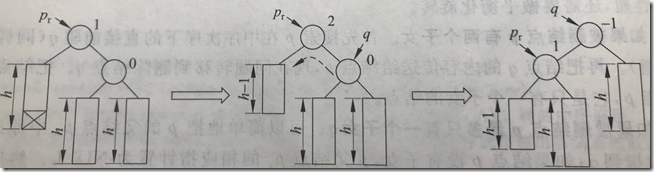
pr的bf=-2，左子树较高，左子树q的bf为0，作右单旋转

旋转后q->bf=pr->bf=0，还要把q->pf改为1，pr->bf改为-1

②pr->bf和q->bf正负号相同的情况：

pr的bf=2，右子树较高，右子树q的bf=1，执行左单旋转，旋转后q->bf=pr->bf=0

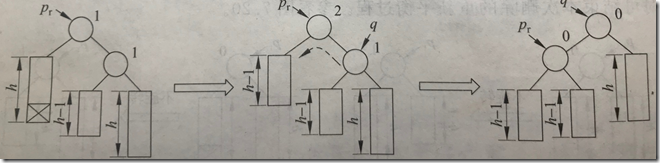
pr的bf=-2，左子树较高，左子树q的bf=-1，执行右单旋转，旋转后q->bf=pr->bf=0

③pr和p的bf正负号相反，执行双旋转，先绕q转一次，再绕pr转一次：

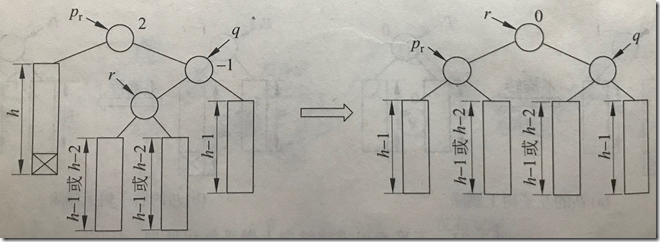
pr的bf=2，右子树较高，右子树q的bf为-1，执行先右后左双旋转

pr的bf=-2，左子树较高，左子树q的bf为1，执行先左后右双旋转

处理后子树高度减少1，继续考察其父结点。

#include <iostream>
#include "stack.h"
using namespace std;

template <class E,class K>
struct AVLNode:public BSTNode<E,K>{
    int bf;   //右子树高度-左子树高度
    AVLNode():left(NULL),right(NULL),bf(){}
    AVLNode(E d,AVLNode<E,K> *l=NULL,AVLNode<E,K> *r=NULL):data(d),left(l),right(r),bf(){}
}

template <class E,class K>
class AVLTree:public BST<E,K>{
public:
    AVLTree():root(NULL){}
    AVLTree(K Ref):RefValue(Ref),root(NULL){}
    bool Insert(E& el){return Insert(root,el);}
    bool Remove(K x,E& el){return Remove(root,el);}
    friend istream& operator>>(istream& in,AVLTree<E,K>& tree);
    friend ostream& operator<<(ostream& out,AVLTree<E,K>& tree);
    int Height()const;
protected:
    AVLNode<E,K> *Search(K x,AVLNode<E,K>* &par)const;
    bool Insert(AVLNode<E,K>* &ptr，E& el);
    bool Remove(AVLNode<E,K>* &ptr,K x,E& el);
    void RotateL(AVLNode<E,K>* &ptr);
    void RotateR(AVLNode<E,K>* &ptr);
    void RotateLR(AVLNode<E,K>* &ptr);
    void RotateRL(AVLNode<E,K>* &ptr);
    int Height(AVLNode<E,K> *ptr)const;
    void AVLTree<E,K>::Traverse(AVLNode<E,K> *ptr,ostream& out)const;
}

template <class E,class K>
void AVLTree<E,K>::RotateL(AVLNode<E,K>* &ptr){
    //右子树比左子树高，对以ptr为根的AVL树做左单旋转，旋转后新根在ptr
    AVLNode<E,K> *subL=ptr;
    ptr=subL->right;  //两个结点平衡因子均为正，需要做左单旋转
    subL->right=ptr->left;
    ptr->left=subL;
    ptr->bf=subL->bf=;
}

template <class E,class K>
void AVLTree<E,K>::RotateR(AVLNode<E,K>* &ptr){
    //左子树比右子树高，对以ptr为根的AVL树做右单旋转，旋转后新根在ptr
    AVLNode<E,K> *subR=ptr;
    ptr=subR->left;    //两个结点平衡因子均为负，需要做右单旋转
    subR->left=ptr->right;
    ptr->right=subR;
    ptr->bf=subR->bf=;
}

template <class E,class K>
void AVLTree<E,K>::RotateLR(AVLNode<E,K>* &ptr){
    AVLNode<E,K> *subR=ptr,*subL=ptr->left;
    ptr=subL->right;
    subL->right=ptr->left;
    ptr->left=subL;
    if(ptr->bf<=) subL->bf=;  //如果ptr->bf原为-1，左单旋转后subL->bf为0
    else subL->bf=-;           //如果ptr->bf原为1，左单旋转后subL->bf为-1
    subR->left=ptr->right;
    ptr->right=subR;
    if(ptr->bf==-) subR->bf=; //如果ptr->bf原为-1，先左后双旋转后subR->bf为1
    else subR->bf=;            //如果ptr->bf原为1，先左后双旋转后subR->bf为0
    ptr->bf=;
}

template <class E,class K>
void AVLTree<E,K>::RotateRL(AVLNode<E,K>* &ptr){
    AVLNode<E,K> *subL=ptr,*subR=ptr->right;
    ptr=subR->left;
    subR->left=ptr->right;
    ptr->right=subR;
    if(ptr->bf>=) subR->bf=;
    else subR->bf=;
    subL->right=ptr->left;
    ptr->left=subL;
    if(ptr->bf==) subL->bf=-;
    else subL->bf=;
    ptr->bf=;
}

template <class E,class K>
bool AVLTree<E,K>::Insert(AVLNode<E,K>* &ptr,E& el){   //改变bf的步骤在旋转中做了，Insert方法中无需再改变
    AVLNode<E,K> *pr=NULL,*p=ptr,*q;
    int d;
    stack<AVLNode<E,K>*> st;
    while(p!=NULL){
        if(el==p->data) return false;
        pr=p;
        st.push(pr);
        if(el<p->data) p=p->left;
        else p=p->right;
    }
    p=new AVLNode<E,K>(el);
    if(p==NULL){
        cerr<<"存储空间不足！"<<endl;
        exit();
    }
    if(pr==NULL){    //空树，新结点成为根结点
        ptr=p;
        return true;
    }
    if(el<pr->data) pr->left=p;
    else pr->right=p;
    while(!st.IsEmpty()){
        st.Pop(pr);
        if(p==pr->left) pr->bf--;  //调整父结点平衡因子
        else pr->bf++;
        //第一种情况，平衡因子为0,说明刚才在pr较矮的子树上插入新结点，结点pr处平衡且高度未变。结点pr到根的路径上所有结点为根的子树高度都未变。可以直接结束重新平衡化的处理。
        if(pr->bf==) break;
        //第二种情况，平衡因子绝对值为1，说明插入前平衡因子为0，插入后以pr为根的子树没有失去平衡，但仍然需要检查结点pr到根的路径上所有结点为根的子树
        if(pr->bf== || pr->bf==-) p=pr;
        //第三种情况，平衡因子绝对值为2,说明新结点在较高的子树上插入，造成了不平衡，需要做平衡化旋转
        else{
            d=(pr->bf<)?-:;
            if(p->bf==d){        //两结点平衡因子同号，单旋转
                if(d==-) RotateR(pr);    //pr的bf为-2，p的bf为1，右单旋转
                else RotateL(pr);         //pr的bf为2，p的bf为-1，左单旋转
            }
            else{
                if(d==-) RotateLR(pr);   //pr的bf为2，p的bf为-1，先右后左旋转
                else RotateRL(pr);        //pr的bf为-2，p的bf为-1，先左后右旋转
            }
            break;  //旋转之后以pr为根的子树高度降低，无需再向上层回溯
        }
    }
    if(st.IsEmpty()) ptr=pr;  //栈空，pr作为新根
    else{
        st.getTop(q);        //栈不空，取出pr的父结点
        if(q->data>pr->data) q->left=pr;
        else q->right=pr;
    }
    return true;
}

template <class E,class K>
istream& operator>>(istream& in,AVLTree<E,K>& Tree){
    E item;
    cout<<"Construct AVL tree:\n";
    cout<<"Input Data(end with"<<Tree.RefValue<<"):";
    in>>item;
    while(item.key!=Tree.RefValue){
        Tree.Insert(item);
        cout<<"Input Data(end with"<<Tree.RefValue<<"):";
        in>>item;
    }
    return in;
}

template <class E,class K>
ostream& operator<<(ostream& out,const AVLTree<E,K>& Tree){
    out<<"Inorder traversal of AVL tree.\n";
    Tree.Traverse(Tree.root,out);
    out<<endl;
    return out;
}

template <class E,class K>
void AVLTree<E,K>::Traverse(AVLNode<E,K> *ptr,ostream& out)const{
    if(ptr!=NULL){
        Traverse(ptr->left,out);
        out<<ptr->data<<'';
        Traverse(ptr->right,out);
    }
}

template <class E,class K>
bool AVLTree<E,K>::Remove(AVLNode<E,K>* &ptr,K x,E& el){
    AVLNode<E,K> *pr=NULL,*p=ptr,*q,*ppr;
    int d,dd=;
    while(p!=NULL){
        if(k==p->data.key) break;
        pr=p;
        st.Push(pr);
        if(k<p->data.key) p=p->left;
        else p=p->right;
    }
    if(p==NULL) return false;
    if(p->left!=NULL && p->right!=NULL){  //被删结点有两个子女
        pr=p;
        st.Push(pr);
        q=p->left;  //在p的左子树找p的直接前驱
        while(q->right!=NULL){
            pr=q;
            st.Push(pr);
            q=q->right;
        }
        p->data=q->data;
        p=q;  //被删结点转换为q，q最多一个子女
    }
    if(p->left!=NULL) q=p->left;  //被删结点只有一个子女或者没有子女
    else q=p->right;
    if(pr==NULL) ptr=q;  //被删结点为根结点，让其子女成为新根
    else{    //被删结点不是根结点
        if(pr->left==p) pr->left=q;   //p的父结点pr原本指向p的指针改指向q
        else pr->right=q;
        while(!st.IsEmpty()){      //重新平衡化
            st.Pop(pr);            //从栈中推出父结点
            if(pr->right==q) pr->bf--;  //调整父结点的平衡因子
            else pr->bf++;
            if(!st.IsEmpty()){
                st.getTop(ppr);     //从栈中取出祖父结点
                dd=(ppr->left==pr)?-:;  //旋转后与上层链接方向
            }
            else dd=;                   //栈空，旋转后不与上层链接
            if(pr->bf== || pr->bf==-)//pr的平衡因子原为0，在它的左/右子树被缩短后，平衡因子变为1或者-1，以pr为根的子树高度没有改变，从pr到根结点的路径上所有结点都不需要调整
                break;
            if(pr->bf!=){
                if(pr->bf<){d=-;q=pr->left;}
                else{d=;q=pr->right;}
                if(q->bf==){
                    if(d==-){  //pr的平衡因子为-2，左子树q的平衡因子为0，执行右单旋转
                        RotateR(pr);
                        pr->bf=;
                        pr->left->bf=-;
                    }
                    else{      //pr的平衡因子为2，右子树q的平衡因子为0，执行左单旋转
                        RotateL(pr);
                        pr->bf=-;
                        pr->right->bf=;
                    }
                    break;
                }
                if(q->bf==d){  //q和pr的平衡因子正负号相同，执行一个单旋转来恢复平衡
                    if(d==-) RotateR(pr);  //pr平衡因子为-2,p平衡因子为-1，右单旋转
                    else RotateL(pr);  //pr平衡因子为2,p平衡因子为1，左单旋转
                }
                else{          //q和pr的平衡因子正负号相反，执行一个双旋转来恢复平衡
                    if(d==-) RotateLR(pr);   //pr的bf=-2，左子树较高，左子树p的bf为1，执行先左后右双旋转
                    else RotateRL(pr);        //pr的bf=2，右子树较高，右子树p的bf为-1，执行先右后左双旋转
                }
                if(dd==-) ppr->left=pr;
                else if(dd==) ppr->right=pr;    //旋转后新根与上层链接
            }
            q=pr;    //pr的平衡因子变为0（较高的子树被缩短了），此时以pr为根的树平衡但高度减少1，需要继续考察pr父结点的平衡状态
        }
        if(st.IsEmpty()) ptr=pr;  //调整到树的根结点
    }
    delete p;
    return true;
}