Logistic 回归-原理及应用

公号：码农充电站pro

主页：https://codeshellme.github.io

上一篇文章介绍了线性回归模型，它用于处理回归问题。

这次来介绍一下 Logistic 回归，中文音译为逻辑回归，它是一个非线性模型，是由线性回归改进而来（所以逻辑回归的名字中带有“回归”二字）。

虽然 Logistic 回归的名字中也有回归二字，但是该算法并非用于回归问题，而是用于处理分类问题，主要用于处理二分类问题，也可以用于处理多分类问题。

1，Logistic 回归模型

Logistic 回归模型将一个事件出现的概率适应到一条S 型曲线上，这条曲线称为 Logistic 曲线。

Logistic 回归函数也叫做 Sigmoid 函数，其基本形式如下：

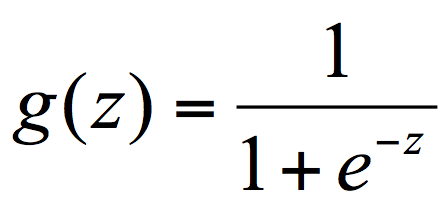
其中：

g(z) 的范围为 (0, 1)
z 的范围为 (-∞, +∞)

g(z) 公式中的自变量 z 就是我们之前介绍的线性模型公式：

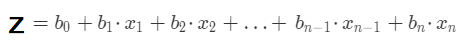
2，画出 Logistic 曲线

NumPy 库中的 linspace(start, stop, num) 方法在 [start, stop] 范围内生成 num 个等距的数字，比如：

>>> import numpy as np

>>>

>>> np.linspace(2.0, 3.0, num=5)    # 在[2.0, 3.0] 范围生成 5 个数字

array([2.  , 2.25, 2.5 , 2.75, 3.  ])

>>>

>>> np.linspace(2.0, 3.0, num=6)    # 在[2.0, 3.0] 范围生成 6 个数字

array([2. , 2.2, 2.4, 2.6, 2.8, 3. ])

为了画出 Logistic 曲线，定义 x，y 如下：

x = np.linspace(-10, 10, 1000)     # 在[10, -10] 范围生成 1000 个数字

y = [1/(1+np.exp(-i)) for i in x]  # 根据 Sigmoid 函数求出 y

用 Matplotlib 画出折线图：

import matplotlib.pyplot as plt

plt.plot(x, y)

plt.show()

S 型曲线如下：

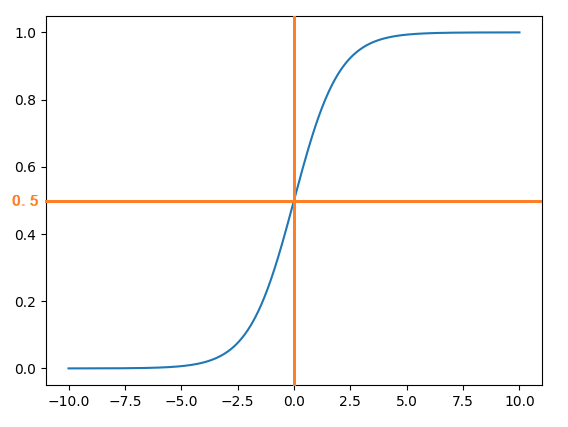
其中橙色的直线是我添加上去的。从上图可以直观的看出S 型曲线的走势，当 x 值在 [-6, 6] 之外时，y 的值变化非常小。

将 Logistic 回归用于二分类问题时，分类为 0 和 1，当 g(z) 大于0.5 时，归入1 类；当 g(z) 小于0.5 时，归入0 类。

3，Logistic 回归的实现

sklearn 库中的 LogisticRegression 类是Logistic 回归的实现。

LogisticRegression 类的原型如下：

LogisticRegression(penalty='l2',

  dual=False, tol=0.0001, C=1.0,

  fit_intercept=True, intercept_scaling=1,

  class_weight=None, random_state=None,

  solver='lbfgs', max_iter=100,

  multi_class='auto', verbose=0,

  warm_start=False, n_jobs=None,

  l1_ratio=None)

来看下其中比较重要的几个参数：

penalty：惩罚项，可取的值有 l1 ，l2，elasticnet，none，默认为 l2。
- l2：当模型参数满足高斯分布的时候，使用 l2。支持 l2 的优化方法有 newton-cg，sag和lbfgs。
- l1：当模型参数满足拉普拉斯分布的时候，使用 l1。在0.19 版本中，sag 支持 l1。
- elasticnet：仅 liblinear 支持 elasticnet。
- none：表示不使用正则化（liblinear 不支持）。
solver：代表的是逻辑回归损失函数的优化方法。有 5 个参数可选，分别为：
- liblinear：coordinate descent (CD)，坐标下降法。适用于数据量小的数据集。
- lbfgs：为默认值，在0.22 版本中改为 liblinear。
- newton-cg：牛顿CG法。
- sag：平均梯度下降法，适用数据量大的数据集。
- saga：随机平均梯度下降法，适用数据量大的数据集。
max_iter：算法收敛的最大迭代次数，默认为 10。
n_jobs：拟合和预测的时候 CPU 的核数，默认是 1。

关于上面的一些参数，也可以参考这里。

4，对鸢尾花数据集进行分类

下面我们使用 Logistic 回归对鸢尾花数据集进行分析。

首先加载数据集：

from sklearn.datasets import load_iris

X, y = load_iris(return_X_y=True)

构建 Logistic 回归模型：

from sklearn.linear_model import LogisticRegression

clf = LogisticRegression() # 创建对象

clf.fit(X, y)              # 拟合模型

对模型的准确率进行评分：

>>> clf.score(X, y)

0.97

可以看到，用 Logistic 回归对鸢尾花数据集进行分类，最终的准确率为 97%，可见效果还是不错的。

5，Logistic 回归处理多分类

Logistic 回归多用于二分类问题，但也可以用于多分类，就像上面对鸢尾花数据集的分析。要让 Logistic 回归处理多分类问题，就要做出一些改进。

一种改进方式是通过多次二分类实现多分类的目的。假如一个数据集有 N 个分类，那就需要训练 N 个二分类模型。对于一个新的特征数据，就需要用这 N 个分类器都对其进行处理，最终选择概率最大的那个分类作为多分类的结果。

另一种方法是将 Logistic 回归改进为 Softmax 回归，Softmax 回归给出的是实例在每一种分类下出现的概率，从而处理多分类任务。

6，总结

Logistic 回归模型是线性回归的改进，用于处理分类问题。实际应用中，Logistic 回归广泛用于广告系统预估点击率，生物统计等领域。

（本节完。）

推荐阅读：

线性回归-如何对数据进行回归分析

AdaBoost 算法-分析波士顿房价数据集

如何用Python 制作词云-对1000首古诗做词云分析

EM 算法-对鸢尾花数据进行聚类

Apriori 算法-如何进行关联规则挖掘

欢迎关注作者公众号，获取更多技术干货。