汉诺塔问题实验--一个简洁的JAVA程序

思路: 这里使用递归法

n==1的时候，直接把它从x移到z位置即可。

如果是n层，我们首先把上面的n- 1层移到y位置,然后把最 下面的那个最大的盘子，移到z位置,然后把y上面放的上面n-1层移到z位置即即可，

我们在移动上面n-1层盘子的时候。先把上面n-2层移到z位置,然后把第n- 1层那个最大的放到y位置,然后把z上面的n-2层移到y位置即可。

我们在移动上面n-2层盘子的时候，先把上面n- 3层移到y位置,然后把最大的那个第n- 2层移到z位置,然后把y上面放的n- 3层放到z位置即可。

我们在移动上面n-3层盘子的时候，........... .递归就完事了!

我们在移动上面2层盘子的时候，首先把上面那个放到y(z)上面,然后把第二层放到z(y)上面，再把y(z) 上面的那一层移到z(y)上面即可。我们在移动上面那一层的时候，n==1
由递推方程的知识可知，该过程的时间复杂性为O(2^n)，64层就要移动2^64-1次盘子。不过这次我们使用程序观察这个变化

这个程序记录了1到36个盘子的时候，Hanoi tower的移动次数，执行时间。为了保证效率，不打印中间结果，只打印最终结果

public class Hanoi {

　　　　/**
　　　　* author:ZhaoKe
　　　　* college: CUST
　　　　*/

　　public long count = 0;
 
    public void hanoi(int n,char a,char b,char c) {
　　　　　　//Hanoi塔问题其实就这几行
        if (n == 1) {
            this.count++;
        }else {
            this.hanoi(n-1, a, c, b);
            this.count++;
            this.hanoi(n-1, b, a, c);
        }
    }
 
    public static void main(String[] args) {
　　　　//程序看起来挺长，大部分代码都是为计算时间服务的
        Hanoi ha = new Hanoi();
        long begin = System.currentTimeMillis();  //获得当前系统时间
        long end = begin;  //循环之前，这里end作为上一轮循环的结束时间，虽然循环还没开始
        for (int i = 1; i <= 36; i++) {
            ha.count = 0;  //循环开始，执行次数置0
            begin = end;  //循环开始，起始时间是上一轮循环的结束时间
            ha.hanoi(i, 'a', 'b', 'c');  //其实Hanoi塔问题只要这一句就够了，其他语句都是为了计算运行时间
            end = System.currentTimeMillis();  //程序结束时间
            System.out.println(i+"个盘子，一共有" +ha.count+ "步");
            System.out.println("程序运行时间：" + (end - begin) + " ms");  //程序运行时间，单位毫秒ms
        }
    }
 
}

运行结果是怎样的呢？

前面盘子比较少的时候就省略了，运行时间都小于1ms，程序显示基本为0ms。

程序运行时间：14 ms
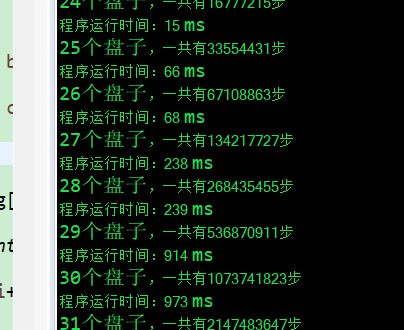
24个盘子，一共有16777215步
程序运行时间：15 ms
25个盘子，一共有33554431步
程序运行时间：66 ms
26个盘子，一共有67108863步
程序运行时间：68 ms
27个盘子，一共有134217727步
程序运行时间：238 ms
28个盘子，一共有268435455步
程序运行时间：239 ms
29个盘子，一共有536870911步
程序运行时间：914 ms
30个盘子，一共有1073741823步
程序运行时间：973 ms
31个盘子，一共有2147483647步
程序运行时间：3681 ms
32个盘子，一共有4294967295步
程序运行时间：3887 ms
33个盘子，一共有8589934591步
程序运行时间：14602 ms
34个盘子，一共有17179869183步
程序运行时间：15504 ms
35个盘子，一共有34359738367步
程序运行时间：58773 ms
36个盘子，一共有68719476735步
程序运行时间：61197 ms

　　可见十分恐怖了。

对照一下打印中间结果多么消耗性能，这里只打印最终结果：

如果将执行的每一步都打印出来的话(使用System.out.println("........."))，n=26的时候就使用了427009ms，比如