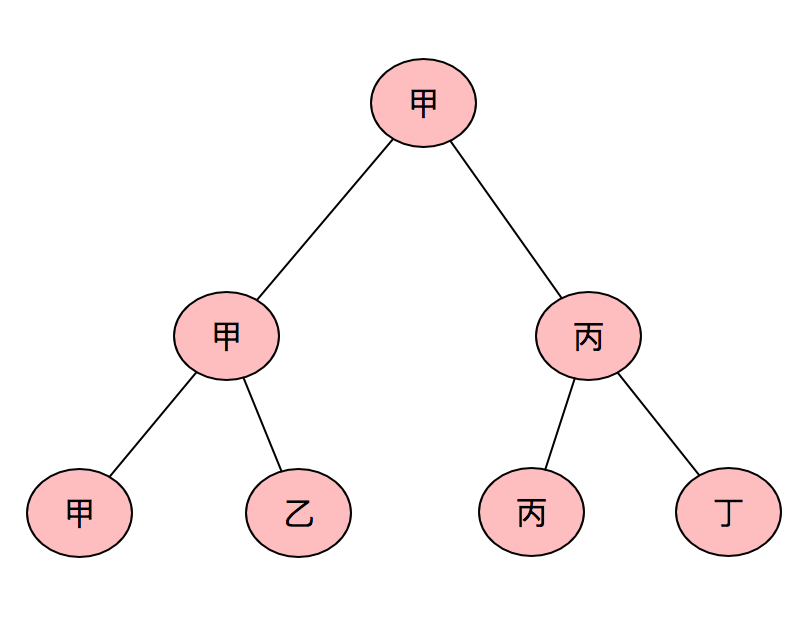
从n个数里面找最大的两个数理论最少需要比较
答案是:n+logn-2
从n个数里面找最大的两个数理论最少需要比较的更多相关文章
- 【C语言】给一组组数,仅仅有两个数仅仅出现了一次,其它全部数都是成对出现的,找出这两个数。
//给⼀组组数,仅仅有两个数仅仅出现了一次.其它全部数都是成对出现的,找出这两个数. #include <stdio.h> int find_one_pos(int num) //找一个为 ...
- 在一个数组中,除了两个数外,其余数都是两两成对出现,找出这两个数,要求时间复杂度O(n),空间复杂度O(1)
题目:在一个数组中,除了两个数外,其余数都是两两成对出现,找出这两个数,要求时间复杂度O(n),空间复杂度O(1) 分析:这道题考察位操作:异或(^),按位与(&),移位操作(>> ...
- 作业帮:给定一个整数数组,找出其中两个数相加等于目标值(去重set)
题目描述 给定一个整数数组,找出其中两个数相加等于目标值 输入 [1,3,5,7,9,11] 10 输出 1,9 3,7 代码: import java.util.HashMap; import ja ...
- Gym 101064 D Black Hills golden jewels 【二分套二分/给定一个序列,从序列中任意取两个数形成一个和,两个数不可相同,要求求出第k小的组合】
D. Black Hills golden jewels time limit per test 2 seconds memory limit per test 256 megabytes input ...
- 由n个元素组成的数组,n-2个数出现了偶数次,两个数出现了奇数次,且这两个数不相等,如何用O(1)的空间复杂度,找出这两个数
思路分析: 方法一:涉及到两个数,就要用到异或定理了:若a^b=x,则a=b^x,b=x^a.对于这道题,假设这两个数分别为a.b,将数组中所有元素异或之后结果为x,因为a!=b,所以x=a^b,且x ...
- 求前n项的斐波那契数列、求两个数的最小公倍数、求两个数的最大公约数
class Fib(object): def __call__(self,n): a=[0,1] for i in range(n-2): an ...
- leetcode:两个数的和||
两个数的和|| 给定一个排序数组,求出其中两个数的和等于指定target时,这两个数在原始数组中的下标,返回的下标从1开始 解题 原始数组已经是升序的,找出其中两个数的和等于target 定义两个指针 ...
- 【剑指offer】和为定值的两个数
转载请注明出处:http://blog.csdn.net/ns_code/article/details/24933341 题目描写叙述: 输入一个递增排序的数组和一个数字S,在数组中查找两个数,是的 ...
- 【剑指offer学习】求和为定值的两个数(拓展)
接着上面一篇文章: http://blog.csdn.net/u013476464/article/details/40651451 接下来我们拓展一下题目,如果数组是乱序的,并且规定数组中的元素所有 ...
随机推荐
- python3 速查参考- python基础 8 -> 面向对象基础:类的创建与基础使用,类属性,property、类方法、静态方法、常用知识点概念(封装、继承等等见下一章)
基础概念 1.速查笔记: #-- 最普通的类 class C1(C2, C3): spam = 42 # 数据属性 def __init__(self, name): # 函数属性:构造函数 self ...
- Python Network Security Programming-1
UNIX口令破解1.程序运行需求: 其中dictionary.txt文件为破解口令的字典文件,passwords.txt文件为临时存放UNIX系统密码的文件 2.程序源码: import crypt ...
- Summary of OAuth 2.0
Summary of OAuth 2.0 1 Problems: This pattern of applications obtaining user passwords obviously has ...
- 《JAVA语言》课问题汇总
一.阅读相应教材,或者使用互联网搜索引擎,弄清楚反码.补码跟原码这几个概念,然后编写示例程序,对正数.负数进行各种位操作,观察输出结果,与手工计算的结果进行比对,看看Java中的数是采用上述哪种码表示 ...
- Go基础:函数多返回值特性
之前在写Python程序的时候,惊叹于它支持多返回值的特性带来的便利性.在学习Go的时候,发现Go也拥有多返回值的特性. 1.基本用法 创建一个多返回值的方法: func getACar() (bra ...
- Petya and Construction Set(图的构造) Codeforces Round #583 (Div. 1 + Div. 2, based on Olympiad of Metropolises)
题意:https://codeforc.es/contest/1214/problem/E 有2n个点,每个2*i和2*i-1的距离必须是Di(<=n),现在让你构造这个树. 思路: 因为Di小 ...
- django进阶版2
目录 批量插入数据 自定义分页器 创建多表关系的3种方法 全自动 全手动 半自动 form组件 如何渲染页面 第一种方式 第二种方式 第三种方式 如何显示错误信息 forms组件钩子函数 局部钩子 全 ...
- Centos7.3安装Mysql5.7.26(glibc即linux通用版)
1.检查防火墙是否关闭 //查看防火墙状态 firewall-cmd --state //关闭防火墙 systemctl stop firewalld systemctl disable firewa ...
- 【IntelliJ IDEA】快捷键
1.System.out.println();的快捷方法 sout然后Alt+Enter或者直接点 2.idea上 重写父类方法的快捷键 Ctrl+O之后,在弹出的上面选择要重写的方法 3.idea ...
- 怎样使用 v-if 实现 html 元素的显示 / 隐藏?
1. 首先, 指令后的引号内是可以写 js 表达式的, 这点很重要. v-if 的用法很简单, 只需要给 v-if = " " 的引号内放一个 布尔值 即可. 注意: v-if 的 ...
