P3355 骑士共存问题【洛谷】(二分图最大独立集变形题) //链接矩阵存图

展开

题目描述

在一个 n*n个方格的国际象棋棋盘上，马（骑士）可以攻击的棋盘方格如图所示。棋盘上某些方格设置了障碍，骑士不得进入

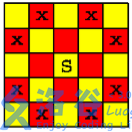
对于给定的 n*n 个方格的国际象棋棋盘和障碍标志，计算棋盘上最多可以放置多少个骑士，使得它们彼此互不攻击

输入格式

第一行有 2 个正整数n 和 m (1<=n<=200, 0<=m<n2)，分别表示棋盘的大小和障碍数。接下来的 m 行给出障碍的位置。每行 2 个正整数，表示障碍的方格坐标。

输出格式

将计算出的共存骑士数输出

输入输出样例

输入

 输出：

思路：本题显然不存在唯一一行对应唯一一列（車的放置）的关系，那么我们将每个“日”字的对角线进行连接 表示这两个端点无法共存。原题转化为:如何去掉最少的点，去掉所有的边

等效于点数-最小点覆盖。那么引出:最大独立集=n-最小点覆盖

类似于【Asteroids POJ - 3041 【最小点覆盖集】】的思想。先求出除了障碍物以外每一个点所能到达的点【到达的点不能是障碍物】。然后在两个相互能到达的点集中 求最小点覆盖{即删掉最小的点使得删掉所有的边【套模板】 }（求出的答案  注意 ans/2   因为是相互的）。然后再套公式：最大独立集=n-最小点覆盖即可。

AC代码：

 #include<bits/stdc++.h>

 //最大独立集=n-最小点覆盖
 using namespace std;
 #define maxn 666
 int dx[]={,,,,-,-,-,-};
 int dy[]={,-,,-,,-,,-};
 int mp[maxn][maxn];
 int match[*];
 int vis[*];
 vector<int> v[**];
 int num[maxn][maxn];
 int flag=;
 int n,m;
 int head[maxn*maxn];
 inline int read(){
     char c = getchar(); int x = , f = ;
     while(c < '' || c > '') {if(c == '-') f = -; c = getchar();}
     while(c >= '' & c <= '') x = x *  + c - '', c = getchar();
     return x * f;
 }
 struct Edge{
     int to,next;
 }e[**];
 void  add(int u,int v){
     flag++;
     e[flag].to=v;
     e[flag].next=head[u];
     head[u]=flag;
 }
 int dfs(int u){
     for(int i=head[u];i;i=e[i].next){
         int temp=e[i].to;
         if(!vis[temp]){
             vis[temp]=;
             if(match[temp]==||dfs(match[temp]))
             {
                 match[temp]=u;
                 return ;
             }
         }
     }
     return ;
 }
 void ok(int x,int y){
     for(int i=;i<;i++){
         int tx=x+dx[i];
         int ty=y+dy[i];
         if(tx>&&ty>&&tx<=n&&ty<=n&&!mp[tx][ty]){
             //v[num[x][y]].push_back(num[tx][ty]);
             //v[num[tx][ty]].push_back(num[x][y]);
             add(num[x][y],num[tx][ty]);
             add(num[tx][ty],num[x][y]);
         }
     }
 }
 int main(){
     //int n,m;
     //scanf("%d%d",&n,&m);
     n=read();
     m=read();
     for(int i=;i<=m;i++){
         int x,y;
         //scanf("%d%d",&x,&y);
         x=read();y=read();
         mp[x][y]=;// 标记不可以走到的点
     }
     int cnt=;
     for(int i=;i<=n;i++)
         for(int j=;j<=n;j++)
             num[i][j]=++cnt;        // 给每一个点编号
     for(int i=;i<=n;i++){
         for(int j=;j<=n;j++){
             if(mp[i][j])
                 continue;
             else{
                 ok(i,j);
             }
         }
     }
     //memset(match,0,sizeof(match));
     int ans=;
     for(int i=;i<=cnt;i++){
     //    memset(vis,0,sizeof(vis));
         for(int i=;i<=cnt;i++)
             vis[i]=;
         if(dfs(i))
             ans++;
     }
     int res=n*n-m-ans/;
     printf("%d\n",res);
     return ;
 }